题目内容
已知双曲线 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率为
的焦点重合,且双曲线的离心率为 .
.
(1)求双曲线的方程;
(2)若有两个半径相同的圆 ,它们的圆心都在
,它们的圆心都在 轴上方且分别在双曲线
轴上方且分别在双曲线 的两条渐近线上,过双曲线右焦点且斜率为
的两条渐近线上,过双曲线右焦点且斜率为 的直线
的直线 与圆
与圆 都相切,求两圆圆心连线的斜率的范围。
都相切,求两圆圆心连线的斜率的范围。
【答案】
20. 解:(1)因为抛物线 的焦点为
的焦点为 ,由已知得
,由已知得 .
.
又

所以双曲线的方程为 5分
5分
(2)直线 的方程为
的方程为 ,双曲线的渐近线方程为
,双曲线的渐近线方程为 7分
7分
由已知可设圆 其中
其中
 直线
直线 与圆
与圆 都相切,
都相切,  , 即
, 即
得 或
或 10分
10分
设两圆 圆心连线斜率为
圆心连线斜率为 ,则
,则 ,
,
当 时,
时, ,
,
当 时,
时,
 故可得
故可得 13分
13分
综上,两圆 圆心连线的斜率的范围为
圆心连线的斜率的范围为 .
14分
.
14分
【解析】略

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
已知双曲线的一个焦点与抛物线x2=20y的焦点重合,且其渐近线的方程为3x±4y=0,则该双曲线的标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为
,则该双曲线的方程为
 B.
B.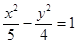 C.
C. D.
D.