Question

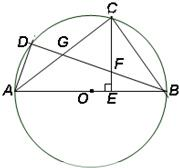
如图，已知AB圆O的直径，C、D是圆O上的两个点，CE⊥AB于E，BD交AC于G，交CE于F，CF=FG．
（Ⅰ）求证：C是劣弧BD的中点；
（Ⅱ）求证：BF=FG．

Answer 1

（I）∵CF=FG
∴∠CGF=∠FCG
∴AB圆O的直径
∴∠ACB=∠ADB=

π

2

∵CE⊥AB
∴∠CEA=

π

2

∵∠CBA=

π

2

-∠CAB，∠ACE=

π

2

-∠CAB
∴∠CBA=∠ACE
∵∠CGF=∠DGA
∴∠DGA=∠ABC∴

π

2

-∠DGA=

π

2

-∠ABC
∴∠CAB=∠DAC
∴C为劣弧BD的中点（5分）
（II）∵∠GBC=

π

2

-∠CGB，∠FCB=

π

2

-∠GCF
∴∠GBC=∠FCB
∴CF=FB
同理可证：CF=GF
∴BF=FG（10分）