题目内容
 如图,正六边形ABCDEF的两个顶点A、D为椭圆的两个焦点,其余4个顶点在椭圆上,则该椭圆的离心率是( ).
如图,正六边形ABCDEF的两个顶点A、D为椭圆的两个焦点,其余4个顶点在椭圆上,则该椭圆的离心率是( ).A、
| ||
B、
| ||
C、
| ||
D、
|
分析:先连接AE,则AE⊥DE.设AD=2c,则可求得DE和AE,进而由椭圆的定义知AE|+|ED|=
c+c求得a,最后根据离心率公式求得答案.
| 3 |
解答:解:连接AE,则AE⊥DE.设|AD|=2c,则|DE|=c,|AE|=
c.
椭圆定义,得2a=|AE|+|ED|=
c+c,
所以e=
=
=
-1,
故选D、
| 3 |
椭圆定义,得2a=|AE|+|ED|=
| 3 |
所以e=
| c |
| a |
| 2 | ||
|
| 3 |
故选D、
点评:本题主要考查了椭圆的简单性质.特别是椭圆定义的应用.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目

 如图,P是边长为1的正六边形ABCDEF所在平面外一点,P在平面ABC内的射影为BF的中点O且PO=1,
如图,P是边长为1的正六边形ABCDEF所在平面外一点,P在平面ABC内的射影为BF的中点O且PO=1, 16、如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中:
16、如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中: 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°;⑤直线PD与平面PAB所成角的余弦值为
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°;⑤直线PD与平面PAB所成角的余弦值为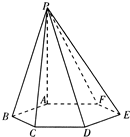 (2012•天门模拟)已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论正确的个数是( )
(2012•天门模拟)已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论正确的个数是( )