题目内容
在单调递增数列 中,
中,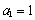 ,
, ,且
,且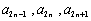 成等差数列,
成等差数列, 成等比数列,
成等比数列,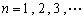 .
.
(1)分别计算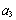 ,
,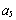 和
和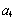 ,
,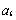 的值;
的值;
(2)求数列 的通项公式(将
的通项公式(将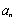 用
用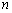 表示);
表示);
(3)设数列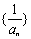 的前
的前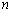 项和为
项和为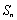 ,证明:
,证明: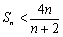 ,
,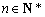 .
.
在单调递增数列 中,
中,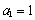 ,
, ,且
,且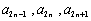 成等差数列,
成等差数列, 成等比数列,
成等比数列,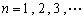 .
.
(1)分别计算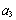 ,
,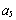 和
和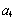 ,
,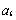 的值;
的值;
(2)求数列 的通项公式(将
的通项公式(将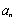 用
用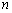 表示);
表示);
(3)设数列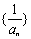 的前
的前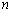 项和为
项和为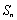 ,证明:
,证明: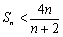 ,
,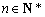 .
.
解:(1)由已知,得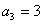 ,
,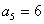 ,
,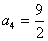 ,
,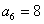 .
.
(2)(证法1)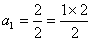 ,
,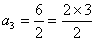 ,
,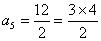 ,……;
,……;
 ,
,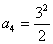 ,
,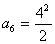 ,…….∴猜想
,…….∴猜想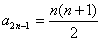 ,
,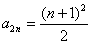 ,
,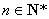 ,
,
以下用数学归纳法证明之.
①当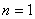 时,
时,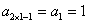 ,
, ,猜想成立;
,猜想成立;
②假设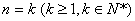 时,猜想成立,即
时,猜想成立,即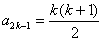 ,
,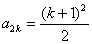 ,那么
,那么
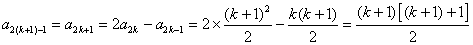
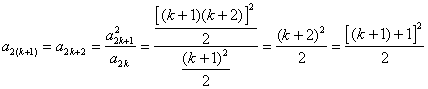
∴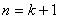 时,猜想也成立.由①②,根据数学归纳法原理,对任意的
时,猜想也成立.由①②,根据数学归纳法原理,对任意的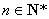 ,猜想成立.
,猜想成立.
∴当 为奇数时,
为奇数时,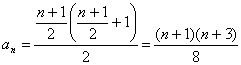 ;
;
当 为偶数时,
为偶数时,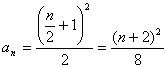 .
.
即数列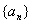 的通项公式为
的通项公式为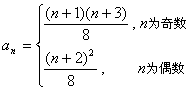 .
.
(3)(解法2)证明:
当 为奇数时,
为奇数时,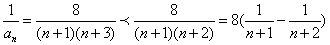
当 为偶数时,.
为偶数时,.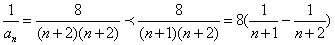
综上,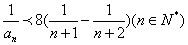
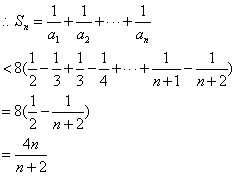
(解法2)由(2),得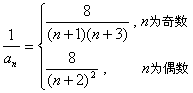 .
.
以下用数学归纳法证明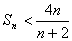 ,
,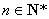 .
.
①当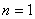 时,
时,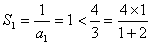 ;
;
当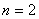 时,
时,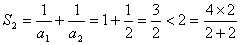 .∴
.∴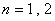 时,不等式成立.
时,不等式成立.
②假设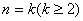 时,不等式成立,即
时,不等式成立,即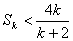 ,
,
那么,当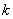 为奇数时,
为奇数时,
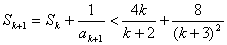
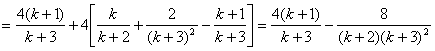
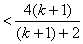 ;
;
当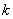 为偶数时,
为偶数时,
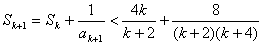
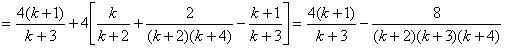
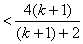 .∴
.∴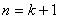 时,不等式也成立.
时,不等式也成立.
综上所述: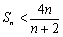

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的展开式中.求:
的展开式中.求: 曲线
曲线 在点
在点 处切线的倾斜角的取值范围为
处切线的倾斜角的取值范围为 ,则点
,则点 到曲线
到曲线 ] B.
] B. C.
C. D.
D.
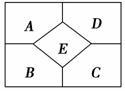
 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 ,点
,点 是直线
是直线 ,则
,则 的最小值为 。
的最小值为 。 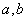 为实数,则一元二次方程
为实数,则一元二次方程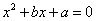 没有实根”时,要做的假设正确的是( )
没有实根”时,要做的假设正确的是( ) 在点
在点 处的切线为
处的切线为 ,曲线
,曲线 在点
在点 处的切线
处的切线 ,若存在
,若存在 ,使得
,使得 ,则实数
,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 的三边
的三边 所对的角分别为
所对的角分别为 ,
, , 则
, 则 的值为( )
的值为( ) B.
B.  C.
C.  D.
D. 
 的通项公式
的通项公式 ,则此数列( )
,则此数列( )