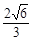题目内容
设F1、F2分别是椭圆 的左、右焦点,B(0,-1).
的左、右焦点,B(0,-1).
(Ⅰ)若P是该椭圆上的一个动点,求 的最大值和最小值;
的最大值和最小值;
(Ⅱ)若C为椭圆上异于B一点,且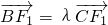 ,求λ的值;
,求λ的值;
(Ⅲ)设P是该椭圆上的一个动点,求△PBF1的周长的最大值.
解:(Ⅰ)易知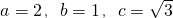 ,所以,
,所以,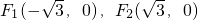 ,
,
设P(x,y),则
=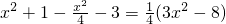 .
.
因为x∈[-2,2],故当x=0,即点P为椭圆短轴端点时, 有最小值-2.
有最小值-2.
当x=±2,即点P为椭圆长轴端点时, 有最大值1.
有最大值1.
(Ⅱ)设C(x0,y0),B(0,-1),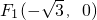 ,由
,由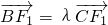 ,得
,得 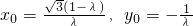 ,
,
又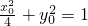 ,所以有 λ2+6λ-7=0,解得λ=-7,(λ=1>0舍去).
,所以有 λ2+6λ-7=0,解得λ=-7,(λ=1>0舍去).
(Ⅲ) 因为|PF1|+|PB|=4-|PF2|+|PB|≤4+|BF2|,∴△PBF1的周长≤4+|BF2|+|BF1|≤8.
所以当P点位于直线BF2与椭圆的交点处时,△PBF1周长最大,最大值为8.
分析:(Ⅰ)根据椭圆的方程,求出焦点的坐标,化简 的 解析式为
的 解析式为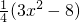 ,结合x∈[-2,2],求得它的最值.
,结合x∈[-2,2],求得它的最值.
(Ⅱ)设C(x0,y0),由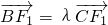 ,用λ 表示 x0,y0,把C(x0,y0)代入椭圆的方程求得λ值.
,用λ 表示 x0,y0,把C(x0,y0)代入椭圆的方程求得λ值.
(Ⅲ) 因为|PF1|+|PB|=4-|PF2|+|PB|≤4+|BF2|,可得△PBF1的周长≤4+|BF2|+|BF1|≤8.
点评:本题考查椭圆的定义、标准方程,以及椭圆的简单性质的应用,两个向量的数量积公式,解得λ=-7把λ=1>0舍去,是解题的易错点.
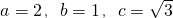 ,所以,
,所以,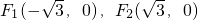 ,
,设P(x,y),则

=
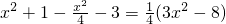 .
.因为x∈[-2,2],故当x=0,即点P为椭圆短轴端点时,
 有最小值-2.
有最小值-2.当x=±2,即点P为椭圆长轴端点时,
 有最大值1.
有最大值1.(Ⅱ)设C(x0,y0),B(0,-1),
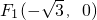 ,由
,由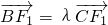 ,得
,得 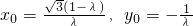 ,
,又
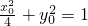 ,所以有 λ2+6λ-7=0,解得λ=-7,(λ=1>0舍去).
,所以有 λ2+6λ-7=0,解得λ=-7,(λ=1>0舍去). (Ⅲ) 因为|PF1|+|PB|=4-|PF2|+|PB|≤4+|BF2|,∴△PBF1的周长≤4+|BF2|+|BF1|≤8.
所以当P点位于直线BF2与椭圆的交点处时,△PBF1周长最大,最大值为8.
分析:(Ⅰ)根据椭圆的方程,求出焦点的坐标,化简
 的 解析式为
的 解析式为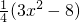 ,结合x∈[-2,2],求得它的最值.
,结合x∈[-2,2],求得它的最值.(Ⅱ)设C(x0,y0),由
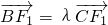 ,用λ 表示 x0,y0,把C(x0,y0)代入椭圆的方程求得λ值.
,用λ 表示 x0,y0,把C(x0,y0)代入椭圆的方程求得λ值.(Ⅲ) 因为|PF1|+|PB|=4-|PF2|+|PB|≤4+|BF2|,可得△PBF1的周长≤4+|BF2|+|BF1|≤8.
点评:本题考查椭圆的定义、标准方程,以及椭圆的简单性质的应用,两个向量的数量积公式,解得λ=-7把λ=1>0舍去,是解题的易错点.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 已知椭圆
已知椭圆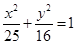 的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则|PM|+|PF1|的最大值为_______
的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则|PM|+|PF1|的最大值为_______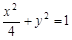 的左、右焦点,P是第一象限内该椭圆上的一点,且
的左、右焦点,P是第一象限内该椭圆上的一点,且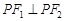 ,求点P的横坐标为( )
,求点P的横坐标为( )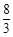 C.
C. D.
D.