题目内容
已知函数f(x)= sin(ωx+φ)(|φ|≤
sin(ωx+φ)(|φ|≤ )的最小正周期为π,将其图象向左平移
)的最小正周期为π,将其图象向左平移 个单位得到函数.f(x)=
个单位得到函数.f(x)= sinωx的图象.
sinωx的图象.
(I)求函数f(x)的单调递增区间;
(II)求函数f(x)在区间[ ]上的最小值和最大值.
]上的最小值和最大值.
解:(Ⅰ)因为函数f(x)= sin(ωx+φ)(|φ|≤
sin(ωx+φ)(|φ|≤ )的最小正周期为π,所以ω=
)的最小正周期为π,所以ω=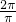 =2,
=2,
故函数f(x)= sin(2x+φ)将其图象向左平移
sin(2x+φ)将其图象向左平移 个单位得到函数.
个单位得到函数.
得到f(x)= sin[2(x+
sin[2(x+ )+φ]=
)+φ]= sin(2x
sin(2x +φ)=
+φ)= sin2x的图象,
sin2x的图象,
所以 =0,φ=-
=0,φ=- ,
,
所以函数f(x)= sin(2x-
sin(2x- ).
).
令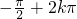 ≤2x-
≤2x-
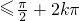 k∈Z
k∈Z
所以 k∈Z.
k∈Z.
所以函数的单调增区间为: ,k∈Z.
,k∈Z.
(Ⅱ)因为函数f(x)= sin(2x-
sin(2x- )在区间[
)在区间[ ]上为单调增函数,
]上为单调增函数,
在区间[ ]上为减函数,
]上为减函数,
又f( )=0,f(
)=0,f( )=
)= ,f(
,f( )=
)= sin(
sin( -
- )=-
)=- sin
sin =-1.
=-1.
故函数f(x)在区间[ ]上的最小值为-1,最大值为
]上的最小值为-1,最大值为 .
.
分析:(I)利用函数的周期求出ω,图象的平移求出φ,求出函数的解析式,利用函数的单调区间.求出函数f(x)的单调递增区间;
(II)确定函数f(x)在区间[ ]上的单调性.然后求出函数的最小值和最大值
]上的单调性.然后求出函数的最小值和最大值
点评:本题考查三角函数的解析式的求法,函数的单调区间的应用,函数最值的求法,考查计算能力.
 sin(ωx+φ)(|φ|≤
sin(ωx+φ)(|φ|≤ )的最小正周期为π,所以ω=
)的最小正周期为π,所以ω=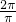 =2,
=2,故函数f(x)=
 sin(2x+φ)将其图象向左平移
sin(2x+φ)将其图象向左平移 个单位得到函数.
个单位得到函数.得到f(x)=
 sin[2(x+
sin[2(x+ )+φ]=
)+φ]= sin(2x
sin(2x +φ)=
+φ)= sin2x的图象,
sin2x的图象,所以
 =0,φ=-
=0,φ=- ,
,所以函数f(x)=
 sin(2x-
sin(2x- ).
).令
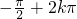 ≤2x-
≤2x-
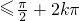 k∈Z
k∈Z 所以
 k∈Z.
k∈Z.所以函数的单调增区间为:
 ,k∈Z.
,k∈Z.(Ⅱ)因为函数f(x)=
 sin(2x-
sin(2x- )在区间[
)在区间[ ]上为单调增函数,
]上为单调增函数,在区间[
 ]上为减函数,
]上为减函数,又f(
 )=0,f(
)=0,f( )=
)= ,f(
,f( )=
)= sin(
sin( -
- )=-
)=- sin
sin =-1.
=-1.故函数f(x)在区间[
 ]上的最小值为-1,最大值为
]上的最小值为-1,最大值为 .
.分析:(I)利用函数的周期求出ω,图象的平移求出φ,求出函数的解析式,利用函数的单调区间.求出函数f(x)的单调递增区间;
(II)确定函数f(x)在区间[
 ]上的单调性.然后求出函数的最小值和最大值
]上的单调性.然后求出函数的最小值和最大值点评:本题考查三角函数的解析式的求法,函数的单调区间的应用,函数最值的求法,考查计算能力.

练习册系列答案
相关题目
