题目内容
已知函数 .
.
(Ⅰ)求函数y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)求函数y=f(x)的单调区间和极值.
解:(Ⅰ)f(0)=1, ,(2分)
,(2分)
f′(0)=0,所以函数y=f(x)在点(0,f(0))处的切线方程为y=1;(14分)
(Ⅱ)函数的定义域为(-1,+∞),
令f'(x)=0,得 ,
,
解得:x=0,x=a-1,(15分)
当a>1时,列表:
可知f(x)的单调减区间是(0,a-1),增区间是(-1,0)∪(a-1,+∞);
极大值为f(0)=1,极小值为 ;(8分)
;(8分)
当0<a<1时,列表:
可知f(x)的单调减区间是(a-1,0),增区间是(-1,a-1)∪(0,+∞);
极大值为 ,极小值为f(0)=1(11分)
,极小值为f(0)=1(11分)
当a=1时,f'(x)≥0,可知函数f(x)在(-1,+∞)上单增,无极值.(13分)
分析:(Ⅰ)把x=0代入函数f(x)的解析式中求出f(0)的值,确定出切点坐标,利用求导法则求出f(x)的导函数,把x=0代入导函数中求出f′(0)的值即为切线的斜率,根据切点坐标和斜率写出切线方程即可;
(Ⅱ)先求出f(x)的定义域,然后领导函数等于0求出x的值,利用x的值分a大于1,a大于0小于1和a=1三种情况讨论导函数的正负确定函数的单调性进而得到函数的单调区间,根据函数的增减性即可得到函数的极大值和极小值.
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导函数的正负判断函数的单调区间且根据函数的增减性得到函数的极值,是一道中档题.学生做第二问时注意求出函数的定义域.
 ,(2分)
,(2分)f′(0)=0,所以函数y=f(x)在点(0,f(0))处的切线方程为y=1;(14分)
(Ⅱ)函数的定义域为(-1,+∞),
令f'(x)=0,得
 ,
,解得:x=0,x=a-1,(15分)
当a>1时,列表:
| x | (-1,0) | 0 | (0,a-1) | a-1 | (a-1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大 | ↘ | 极小 | ↗ |
极大值为f(0)=1,极小值为
 ;(8分)
;(8分)当0<a<1时,列表:
| x | (-1,a-1) | a-1 | (a-1,0) | 0 | (0,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大 | ↘ | 极小 | ↗ |
极大值为
 ,极小值为f(0)=1(11分)
,极小值为f(0)=1(11分)当a=1时,f'(x)≥0,可知函数f(x)在(-1,+∞)上单增,无极值.(13分)
分析:(Ⅰ)把x=0代入函数f(x)的解析式中求出f(0)的值,确定出切点坐标,利用求导法则求出f(x)的导函数,把x=0代入导函数中求出f′(0)的值即为切线的斜率,根据切点坐标和斜率写出切线方程即可;
(Ⅱ)先求出f(x)的定义域,然后领导函数等于0求出x的值,利用x的值分a大于1,a大于0小于1和a=1三种情况讨论导函数的正负确定函数的单调性进而得到函数的单调区间,根据函数的增减性即可得到函数的极大值和极小值.
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导函数的正负判断函数的单调区间且根据函数的增减性得到函数的极值,是一道中档题.学生做第二问时注意求出函数的定义域.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 .
.
(1)求 的最小值;
的最小值;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间.设 ,试问函数
,试问函数 在
在 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在 上为增函数,则称
上为增函数,则称 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为 .
.
(Ⅰ)已知函数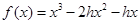 ,若
,若 且
且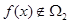 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 且
且 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证: ;
;
(Ⅲ)定义集合
请问:是否存在常数 ,使得
,使得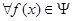 ,
, ,有
,有 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.


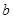
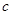




 ,编写一个程序求函数值.
,编写一个程序求函数值. 试画出求函数值的程序框图.
试画出求函数值的程序框图.