题目内容
(本小题满分12分)已知函数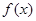 =
=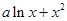 (
(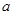 为实常数).
为实常数).
(1)若函数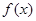 在
在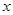 =1处与
=1处与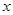 轴相切,求实数
轴相切,求实数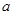 的值.
的值.
(2)若存在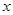 ∈[1,
∈[1,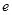 ],使得
],使得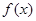 ≤
≤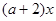 成立,求实数
成立,求实数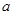 的取值范围.
的取值范围.
【答案】
(1)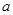 =
= ;(2)a的取值范围是
;(2)a的取值范围是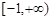 .
.
【解析】(1)先求出原函数的导数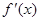 =
=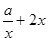 =欲求出切线方程,只须求出其斜率即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.列出关于a的方程求得a的值
=欲求出切线方程,只须求出其斜率即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.列出关于a的方程求得a的值
(2)存在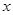 ∈[1,
∈[1,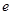 ],使得
],使得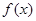 ≤
≤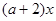 成立,
成立,
不等式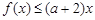 , 可化为
, 可化为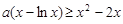 .
.
∵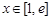 , ∴
, ∴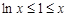 且等号不能同时取,所以
且等号不能同时取,所以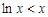 ,即
,即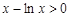 ,
,
因而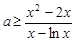 (
(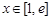 )构造函数利用导数求解最大值即可。
)构造函数利用导数求解最大值即可。
解:(1)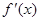 =
=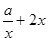 =
=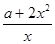 ,由
,由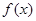 在
在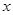 =1处与
=1处与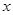 轴相切知,
轴相切知,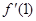 =0,即
=0,即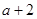 =0
=0
解得,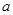 =
= ;
;
(2)不等式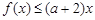 , 可化为
, 可化为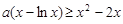 .
.
∵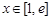 , ∴
, ∴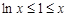 且等号不能同时取,所以
且等号不能同时取,所以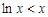 ,即
,即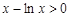 ,
,
因而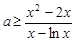 (
(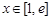 )
)
令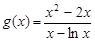 (
(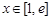 ),又
),又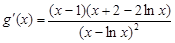 ,
,
当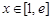 时,
时,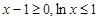 ,
,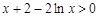 ,
,
从而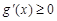 (仅当x=1时取等号),所以
(仅当x=1时取等号),所以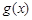 在
在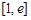 上为增函数,
上为增函数,
故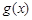 的最小值为
的最小值为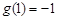 ,所以a的取值范围是
,所以a的取值范围是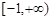 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目