题目内容
10.已知抛物线C:y2=2px (p>0)的焦点为F,过点F倾斜角为60°的直线l与抛物线C在第一、四象限分别交于A、B两点,则$\frac{{|{AF}|}}{{|{BF}|}}$的值等于3.分析 设出A、B坐标,利用焦半径公式求出|AB|,结合x1x2=$\frac{{p}^{2}}{4}$,求出A、B的坐标,然后求其比值.
解答 解:设A(x1,y1),B(x2,y2),则y12=2px1,y22=2px2,
|AB|=x1+x2+p=$\frac{2p}{si{n}^{2}θ}$=$\frac{8}{3}$p,即有x1+x2=$\frac{5}{3}$p,
由直线l倾斜角为60°,
则直线l的方程为:y-0=$\sqrt{3}$(x-$\frac{p}{2}$),
即y=$\sqrt{3}$x-$\frac{\sqrt{3}}{2}$p,联立抛物线方程,
消去y并整理,得
12x2-20px+3p2=0,
则x1x2=$\frac{{p}^{2}}{4}$,可得x1=$\frac{3}{2}$p,x2=$\frac{1}{6}$p,
则$\frac{|AF|}{|BF|}$=$\frac{\frac{3}{2}p+\frac{1}{2}p}{\frac{1}{2}p+\frac{1}{6}p}$=3,
故答案为:3.
点评 本题考查直线的倾斜角,抛物线的简单性质,考查学生分析问题解决问题的能力,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
1.2014巴西世界杯结束后,某网站针对世界杯情况进行了调查,参与调查的人主要集中在[20,50]岁之间,若规定;观看世界杯直播32场(含)以下者,称为“非球迷”,观看比赛直播超过32场这成为“球迷”,得到如下统计表:
若参与调查的“非球迷”总人数为7600人.
(1)求a的值;
(2)从年龄在[20,35)的“球迷”中按照年龄区间分层抽样的方法抽取20人
①从这20人中随机抽取2人,求这2人恰好属于同一年龄区间的概率
②从这20人中随机抽取2人,用ζ表示年龄在[30,35)之间的人数,求ξ的分布列及期望值E(ξ).
| 分组编号 | 年龄分组 | 球迷 | 所占比例 |
| 1 | [20,25] | 1200 | 0.5 |
| 2 | [25,30] | 1800 | 0.6 |
| 3 | [30,35] | 1000 | 0.5 |
| 4 | [35,40] | a | 0.4 |
| 5 | [40,45] | 300 | 0.2 |
| 6 | [45,50] | 200 | 0.1 |
(1)求a的值;
(2)从年龄在[20,35)的“球迷”中按照年龄区间分层抽样的方法抽取20人
①从这20人中随机抽取2人,求这2人恰好属于同一年龄区间的概率
②从这20人中随机抽取2人,用ζ表示年龄在[30,35)之间的人数,求ξ的分布列及期望值E(ξ).
5.设m,n是两条不同的直线,α,β是两个不同的平面,则( )
| A. | 若m∥α,m∥β,则α∥β | B. | 若m∥α,m∥n,则n∥α | C. | 若m⊥α,m∥β,则α⊥β | D. | 若m∥α,n?α,则m∥n |
17.已知函数f(x)=sinπx和函数g(x)=cosπx在区间[0,2]上的图象交于A,B两点,则△OAB面积是( )
| A. | $\frac{3\sqrt{2}}{8}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{5\sqrt{2}}{8}$ | D. | $\frac{3\sqrt{2}}{4}$ |
17.已知函数f(x)=$\frac{1}{x+2}$-k|x|({k∈R})有三个不同的零点,则实数k的取值范围是( )
| A. | (0,1) | B. | (0,2) | C. | (1,+∞) | D. | (2,+∞) |
 ,
,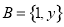 ,且
,且 ,则
,则 ( )
( )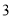 B.
B.
 D.
D.