题目内容
已知函数f(x)是(-∞,+∞)上的奇函数,且f(x)的图象关于直线x=1对称,当x∈[-1,0]时,f(x)=1- ,则f(2012)+f(2013)=________.
,则f(2012)+f(2013)=________.
1
分析:由函数的对称性可得f(x)=f(2-x),再由奇偶性可得f(x)=-f(x-2),由此可推得函数的周期,根据周期性可把f(2012),f(2013)转化为已知区间上求解.
解答:因为f(x)图象关于x=1对称,所以f(x)=f(2-x),
又f(x)为奇函数,所以f(2-x)=-f(x-2),即f(x)=-f(x-2),
则f(x+4)=-f(x+2)=-[-f(x)]=f(x),
故4为函数f(x)的一个周期,
从而f(2012)+f(2013)=f(0)+f(1),
而f(0)=1-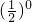 =0,f(1)=-f(-1)=-[1-
=0,f(1)=-f(-1)=-[1- ]=1,
]=1,
故f(0)+f(1)=1,即f(2012)+f(2013)=1,
故答案为:1.
点评:本题考查函数的奇偶性、周期性、对称性及其应用,考查函数求值,解决本题的关键是利用已知条件推导函数周期.
分析:由函数的对称性可得f(x)=f(2-x),再由奇偶性可得f(x)=-f(x-2),由此可推得函数的周期,根据周期性可把f(2012),f(2013)转化为已知区间上求解.
解答:因为f(x)图象关于x=1对称,所以f(x)=f(2-x),
又f(x)为奇函数,所以f(2-x)=-f(x-2),即f(x)=-f(x-2),
则f(x+4)=-f(x+2)=-[-f(x)]=f(x),
故4为函数f(x)的一个周期,
从而f(2012)+f(2013)=f(0)+f(1),
而f(0)=1-
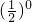 =0,f(1)=-f(-1)=-[1-
=0,f(1)=-f(-1)=-[1- ]=1,
]=1,故f(0)+f(1)=1,即f(2012)+f(2013)=1,
故答案为:1.
点评:本题考查函数的奇偶性、周期性、对称性及其应用,考查函数求值,解决本题的关键是利用已知条件推导函数周期.

练习册系列答案
相关题目