题目内容
连接双曲线
与
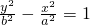的四个顶点构成的四边形的面积为S1，连接它们的四个焦点构成的四边形的面积为S2，则S1：S2的最大值是
- A.2
- B.1
- C.
- D.
C
分析：根据对称性，两个四边形的面积都可以分为四个全等的直角三角形的面积，两个面积的比值用a，b表示出来，再根据基本不等式求最大值．
解答：设双曲线的右顶点为A，其坐标是（a，0），由焦点为C，坐标为（
，0）；
设双曲线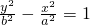上顶点为B，坐标为（0，b），上焦点为D，坐标为（0，）．O为坐标原点．
则S1=4S△OAB=2ab，S2=4S△OCD=2（a2+b2），
所以
≤
=．
故选C．
点评：本题考查双曲线的简单几何性质和使用基本不等式求最值，考查计算能力．
分析：根据对称性，两个四边形的面积都可以分为四个全等的直角三角形的面积，两个面积的比值用a，b表示出来，再根据基本不等式求最大值．
解答：设双曲线
的右顶点为A，其坐标是（a，0），由焦点为C，坐标为（，0）；设双曲线
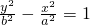上顶点为B，坐标为（0，b），上焦点为D，坐标为（0，）．O为坐标原点．则S1=4S△OAB=2ab，S2=4S△OCD=2（a2+b2），
所以
≤=．故选C．
点评：本题考查双曲线的简单几何性质和使用基本不等式求最值，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
=________．
+
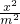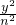=1（m＞0，n＞0）的右焦点与抛物线y2=8x的焦点相同，离心率为
+
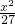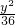=1有相同的焦点，且与椭圆相交，一个交点A的纵坐标为4，求此双曲线的标准方程．
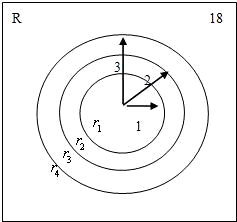山姆的意大利馅饼屋中设有一个投镖靶 该靶为正方形板．边长为18厘米，挂于前门附近的墙上，顾客花两角伍分的硬币便可投一镖并可有机会赢得一种意大利 馅饼中的一个，投镖靶中画有三个同心圆，圆心在靶的中心，当投镖击中半径为1厘米的最内层圆域时．可得到一个大馅饼；当击中半径为1厘米到2厘米之间的环域时，可得到一个中馅饼；如果击中半径为2厘米到3厘米之间的环域时，可得到一个小馅饼，如果击中靶上的其他部分，则得不到谄饼，我们假设每一个顾客都能投镖中靶，并假设每个圆的周边线没有宽度，即每个投镖不会击中线上，试求一顾客将嬴得：
附近的平均变化率为k1，k2，则k1，k2的大小关系为
，
，
，则
的定义域为