题目内容
已知函数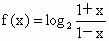
，
．
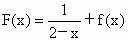(1)设F(x)的反函数为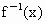
，则方程
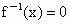有解吗?若有解，求出其解；若没有解，则说明理由．
(2)若f(x)的反函数为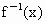
，则对任意的自然数n(n>2)，是否都有
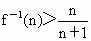成立?并说明理由．
答案：略
解析：
解析：
|
(1) 由 ，且2－x 0，得－1＜x＜1．而 在(－1，1)上递增，∴ 在(－1，1)上递增．又 在(－1，1)上递增，∴F(x)在(－1，1)上单调递增．故F(x)存在反函数．且 也是单调递增函数．又 ，∴ ，而 单调递增．故方程 有惟一解 ．
(2) 由 ，得 ．又 且 在(0，＋∞)上单调递增．作函数 与y=2x＋1的图象如图所示，由图可知当x≥3时，函数 的图象总在函数y=2x＋1的图象的上方．
∴当 n＞2且 时，恒有 成立．即 恒成立．
|
练习册系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
已知函数f(x)=
+
的定义域是（ ）
| 1-x2 |
| x2-1 |
| A、[-1，1] |
| B、{-1，1} |
| C、（-1，1） |
| D、（-∞，-1]∪[1，+∞） |