题目内容
已知f(x)=x3+ax2-x+2,g(x)=xlnx.(1)如果函数f(x)的单调递减区间为
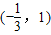 ,求函数f(x)的解析式;
,求函数f(x)的解析式;(2)在(1)的条件下,求函数y=f(x)的图象过点P(1,1)的切线方程;
(3)对一切的x∈(0,+∞),f'(x)+2≥2g(x)恒成立,求实数a的取值范围.
【答案】分析:(1)根据函数的单调区间可知- ,1是导函数所对应方程的两个根,从而可求出a的值;
,1是导函数所对应方程的两个根,从而可求出a的值;
(2)设切点坐标是M(x,y)(x≠1),然后根据在该点处的导数等于两点的斜率建立等式关系,从而求出x的值,即可求出切线方程;
(3)3x2+2ax-1+2≥2xlnx在x∈(0,+∞)上恒成立将a分离可得a≥lnx-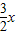 -
-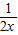 ,设h(x)=lnx-
,设h(x)=lnx-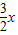 -
-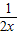 ,利用导数研究h(x)的最大值,可求出a的取值范围.
,利用导数研究h(x)的最大值,可求出a的取值范围.
解答:解:(1)f'(x)=3x2+2ax-1
由题意3x2+2ax-1>0的解集是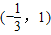 即3x2+2ax-1=0的两根分别是-
即3x2+2ax-1=0的两根分别是- ,1
,1
将x=1或- 代入方程3x2+2ax-1=0得a=-1,
代入方程3x2+2ax-1=0得a=-1,
∴f(x)=x3-x2-x+2
(2)设切点坐标是M(x,y)(x≠1).有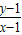 =3x2-2x-1
=3x2-2x-1
将y=x3-x2-x+2代入上式整理得
得x=1或x=0.
函数f(x)=x3-x2-x+2的图象过点P(1,1)的切线方程为x+y-2=0或y=1.
(3)由题意:3x2+2ax-1+2≥2xlnx在x∈(0,+∞)上恒成立
即3x2+2ax+1≥2xlnx可得a≥lnx-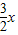 -
-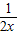
设h(x)=lnx-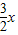 -
-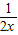 ,则h′(x)=-
,则h′(x)=-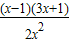
令h′(x)=0,得x=1,x=- (舍),当0<x<1时,h′(x)>0;当x>1时,h′(x)<0
(舍),当0<x<1时,h′(x)>0;当x>1时,h′(x)<0
∴当x=1时,h(x)取得最大值,h(x)max=-2,.
∴a≥-2,即a的取值范围是[-2,+∞).
点评:本题主要考查了利用导数研究函数的单调性以及利用导数研究函数在某点切线方程,同时考查了转化的思想和计算能力,属于难题.
 ,1是导函数所对应方程的两个根,从而可求出a的值;
,1是导函数所对应方程的两个根,从而可求出a的值;(2)设切点坐标是M(x,y)(x≠1),然后根据在该点处的导数等于两点的斜率建立等式关系,从而求出x的值,即可求出切线方程;
(3)3x2+2ax-1+2≥2xlnx在x∈(0,+∞)上恒成立将a分离可得a≥lnx-
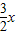 -
-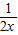 ,设h(x)=lnx-
,设h(x)=lnx-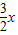 -
-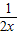 ,利用导数研究h(x)的最大值,可求出a的取值范围.
,利用导数研究h(x)的最大值,可求出a的取值范围.解答:解:(1)f'(x)=3x2+2ax-1
由题意3x2+2ax-1>0的解集是
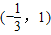 即3x2+2ax-1=0的两根分别是-
即3x2+2ax-1=0的两根分别是- ,1
,1将x=1或-
 代入方程3x2+2ax-1=0得a=-1,
代入方程3x2+2ax-1=0得a=-1,∴f(x)=x3-x2-x+2
(2)设切点坐标是M(x,y)(x≠1).有
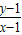 =3x2-2x-1
=3x2-2x-1将y=x3-x2-x+2代入上式整理得

得x=1或x=0.
函数f(x)=x3-x2-x+2的图象过点P(1,1)的切线方程为x+y-2=0或y=1.
(3)由题意:3x2+2ax-1+2≥2xlnx在x∈(0,+∞)上恒成立
即3x2+2ax+1≥2xlnx可得a≥lnx-
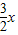 -
-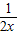
设h(x)=lnx-
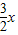 -
-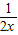 ,则h′(x)=-
,则h′(x)=-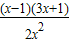
令h′(x)=0,得x=1,x=-
 (舍),当0<x<1时,h′(x)>0;当x>1时,h′(x)<0
(舍),当0<x<1时,h′(x)>0;当x>1时,h′(x)<0∴当x=1时,h(x)取得最大值,h(x)max=-2,.
∴a≥-2,即a的取值范围是[-2,+∞).
点评:本题主要考查了利用导数研究函数的单调性以及利用导数研究函数在某点切线方程,同时考查了转化的思想和计算能力,属于难题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目