题目内容
已知圆C：x2+y2=12，直线l：4x+3y=25．求圆C上任意一点A到直线l的距离小于2的概率．
【答案】分析：根据平行线的距离公式，算出到直线l：4x+3y=25的距离等于2且与已知圆相交的直线为直线l'：4x+3y-15=0．设l'交圆x2+y2=12于E、B两点，由图形观察可得当动点A位于劣弧BE上时点A到直线l的距离小于2．由此利用点到直线的距离公式，结合垂径定理和三角函数的定义算出∠EOB=60°，即可得到所求概率．
解答：解：设直线l'：4x+3y-C=0，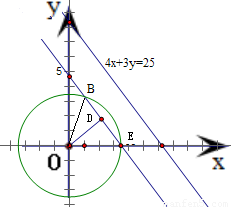
l'与直线l：4x+3y=25的距离等于2，且与已知圆相交，
可得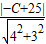
=2，解之得C=15或40
∵C＜25，可得C=15
∴到直线l：4x+3y=25的距离等于2且与已知圆相交的直线
为直线l'：4x+3y-15=0，
设l'交圆x2+y2=12于E、B两点，过圆心作EB的垂线，垂足为D，
则D为EB的中点，
∵|OD|=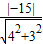
=3，
∴Rt△EOD中，cos∠EOD=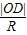
=
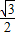，得∠EOD=30°
由此可得∠EOB=60°
当圆C上任意一点A到直线l的距离小于2时，点A位于劣弧BE上，
因此，所求概率为P=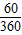
=
．
点评：本题给出直线与圆，求圆上动点到直线的距离小于2的概率．着重考查了点到直线的距离公式、三角函数的定义和几何概型及其计算等知识，属于中档题．
解答：解：设直线l'：4x+3y-C=0，
l'与直线l：4x+3y=25的距离等于2，且与已知圆相交，
可得
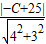=2，解之得C=15或40∵C＜25，可得C=15
∴到直线l：4x+3y=25的距离等于2且与已知圆相交的直线
为直线l'：4x+3y-15=0，
设l'交圆x2+y2=12于E、B两点，过圆心作EB的垂线，垂足为D，
则D为EB的中点，
∵|OD|=
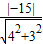=3，∴Rt△EOD中，cos∠EOD=
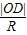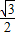=，得∠EOD=30°由此可得∠EOB=60°
当圆C上任意一点A到直线l的距离小于2时，点A位于劣弧BE上，
因此，所求概率为P=
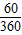=．点评：本题给出直线与圆，求圆上动点到直线的距离小于2的概率．着重考查了点到直线的距离公式、三角函数的定义和几何概型及其计算等知识，属于中档题．
练习册系列答案
精英口算卡系列答案
相关题目
（2009•普陀区一模）如图，已知圆C：x2+y2=r2与x轴负半轴的交点为A．由点A出发的射线l的斜率为k，且k为有理数．射线l与圆C相交于另一点B．