题目内容
设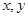 满足约束条件:
满足约束条件: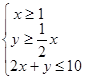 的可行域为
的可行域为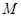
1)在所给的坐标系中画出可行域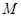 (用阴影表示,并注明边界的交点或直线);
(用阴影表示,并注明边界的交点或直线);
2)求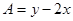 的最大值与
的最大值与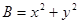 的最小值;
的最小值;
3)若存在正实数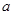 ,使函数
,使函数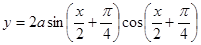 的图象经过区域
的图象经过区域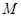 中的点,
中的点,
求这时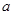 的取值范围.
的取值范围.
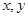 满足约束条件:
满足约束条件: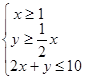 的可行域为
的可行域为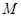
1)在所给的坐标系中画出可行域
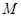 (用阴影表示,并注明边界的交点或直线);
(用阴影表示,并注明边界的交点或直线);2)求
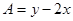 的最大值与
的最大值与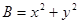 的最小值;
的最小值;3)若存在正实数
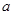 ,使函数
,使函数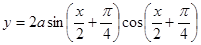 的图象经过区域
的图象经过区域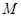 中的点,
中的点,求这时
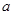 的取值范围.
的取值范围.解:1)
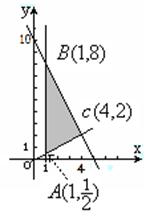
可行域M为如图
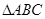 ; 2)
; 2)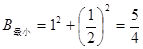 . 3)
. 3)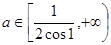 .
.第一问中,利用不等式组表示的得到区域图形
第二问中∵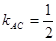
又∵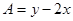 ∴
∴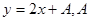 是
是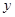 轴的截距,
轴的截距,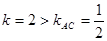
∴过点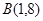 时,
时,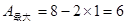
∵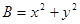 是表示区域M上的点
是表示区域M上的点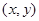 到原点O
到原点O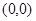 距离的平方.
距离的平方.
如图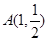 使所求距离的平方最小,∴
使所求距离的平方最小,∴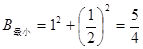
第三问中,∵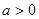
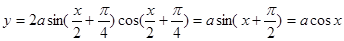 ]
]
过区域M中的点,而区域中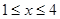
又∵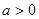 ,函数
,函数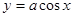 图象过点
图象过点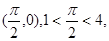
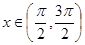 时,
时,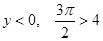
∴满足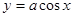 过区域M中的点,只须图象与射线
过区域M中的点,只须图象与射线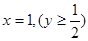 有公共点.
有公共点.
∴只须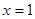 时,
时, 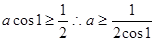
∴所求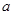 的取值范围是
的取值范围是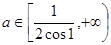
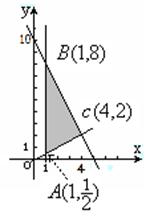
解:1)阴影部分如图
由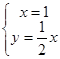 ,得
,得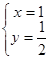 ∴
∴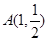
由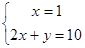 ,得
,得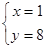 ∴
∴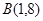
由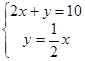 ,得
,得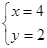 ∴
∴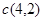
可行域M为如图
2)∵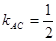
又∵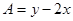 ∴
∴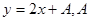 是
是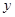 轴的截距,
轴的截距,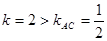
∴过点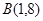 时,
时,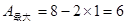
∵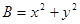 是表示区域M上的点
是表示区域M上的点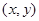 到原点O
到原点O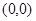 距离的平方.
距离的平方.
如图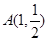 使所求距离的平方最小,∴
使所求距离的平方最小,∴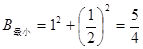 .
.
3)∵
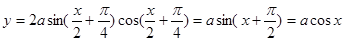
过区域M中的点,而区域中
又∵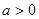 ,函数
,函数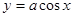 图象过点
图象过点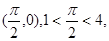
当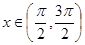 时,
时,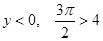
∴满足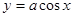 过区域M中的点,只须图象与射线
过区域M中的点,只须图象与射线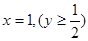 有公共点.
有公共点.
∴只须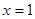 时,
时, 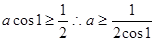
∴所求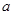 的取值范围是
的取值范围是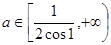 .
.
第二问中∵
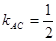
又∵
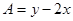 ∴
∴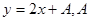 是
是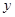 轴的截距,
轴的截距,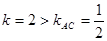
∴过点
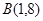 时,
时,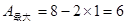
∵
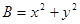 是表示区域M上的点
是表示区域M上的点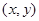 到原点O
到原点O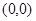 距离的平方.
距离的平方.如图
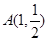 使所求距离的平方最小,∴
使所求距离的平方最小,∴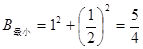
第三问中,∵
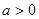
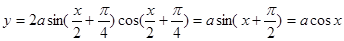 ]
]过区域M中的点,而区域中
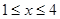
又∵
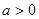 ,函数
,函数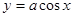 图象过点
图象过点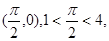
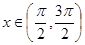 时,
时,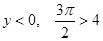
∴满足
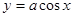 过区域M中的点,只须图象与射线
过区域M中的点,只须图象与射线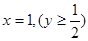 有公共点.
有公共点.∴只须
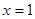 时,
时, 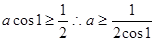
∴所求
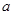 的取值范围是
的取值范围是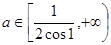
解:1)阴影部分如图

由
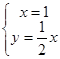 ,得
,得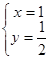 ∴
∴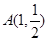
由
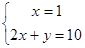 ,得
,得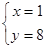 ∴
∴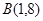
由
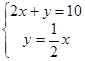 ,得
,得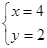 ∴
∴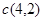
可行域M为如图
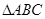
2)∵
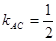
又∵
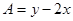 ∴
∴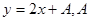 是
是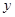 轴的截距,
轴的截距,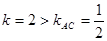
∴过点
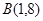 时,
时,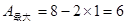
∵
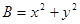 是表示区域M上的点
是表示区域M上的点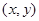 到原点O
到原点O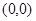 距离的平方.
距离的平方.如图
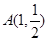 使所求距离的平方最小,∴
使所求距离的平方最小,∴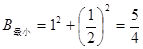 .
.3)∵
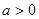
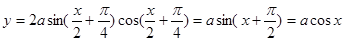
过区域M中的点,而区域中
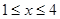
又∵
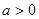 ,函数
,函数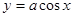 图象过点
图象过点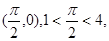
当
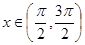 时,
时,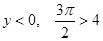
∴满足
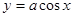 过区域M中的点,只须图象与射线
过区域M中的点,只须图象与射线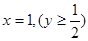 有公共点.
有公共点.∴只须
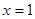 时,
时, 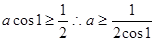
∴所求
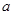 的取值范围是
的取值范围是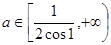 .
.
练习册系列答案
相关题目
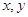 满足约束条件
满足约束条件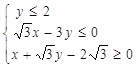 ,则目标函数
,则目标函数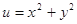 的最大值
的最大值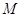 与最小值
与最小值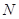 的比
的比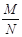 = ( )
= ( )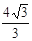
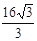
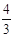
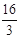
 则2x+3y的最大值为
则2x+3y的最大值为 在曲线
在曲线 上,点
上,点 在不等式组
在不等式组 所表示的平面区域内,那么
所表示的平面区域内,那么 的最小值是( )
的最小值是( )



 则
则 的最小值是______.
的最小值是______. 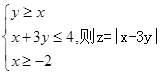 的最大值为( )
的最大值为( )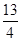
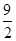
 的图象与x轴所围成的封闭图形的面积( )
的图象与x轴所围成的封闭图形的面积( )

 不在平面区域
不在平面区域 内,则
内,则 的取值范围是( )
的取值范围是( )


