题目内容
（本小题12分）设等差数列{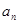
}的前
项和为
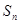，已知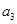
＝
，
．
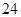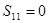(1) 求数列{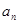}的通项公式； （2）当n为何值时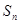，最大，并求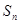的最大值．
【答案】
（1）
.（2）当
或
时，
最大，且的最大值为120.
【解析】(1)由
＝
，
可建立关于a1和d的方程，求出a1和d的值，从而确定{
}的通项公式.
（2）在（1）的基础上，可求出
,从而利用二次函数的性质可求出其最大值，要注意n取正整数.
（1）依题意有
，解之得
，∴.
（2）由（1）知，
＝40，，
∴ ＝
＝
＝－4
＋121，
故当或时，最大，且的最大值为120.
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
中，底面
为矩形，侧面
底面
，
，
．
；
为等边三角形，求二面角
的大小．
m，试建立S与x的函数关系；
，求数列{bn}的前N项和Tn。
克，这些球等可能地从袋里取出（不受重量、号码的影响）。
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的，现投掷骰子根据其点数决定棋子是否移动：若投出的点数是偶数，棋子移动到另一个顶点；若投出的点数是奇数，则棋子不动.若棋子的初始位置在顶点A.
.求