题目内容
设函数f(x)=lnx-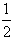 ax2-bx,
ax2-bx,
(1)当a=b=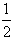 时,求f(x)的最大值;
时,求f(x)的最大值;
(2)令F(x)=f(x)+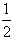 ax2+bx+
ax2+bx+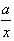 ,(0<x≤3),其图象上任意一点P(x0,y0)处切线的斜率k≤
,(0<x≤3),其图象上任意一点P(x0,y0)处切线的斜率k≤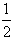 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)当a=0,b=-1,方程2mf(x)=x2有唯一实数解,求正数m的值。
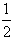 ax2-bx,
ax2-bx,(1)当a=b=
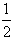 时,求f(x)的最大值;
时,求f(x)的最大值;(2)令F(x)=f(x)+
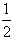 ax2+bx+
ax2+bx+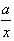 ,(0<x≤3),其图象上任意一点P(x0,y0)处切线的斜率k≤
,(0<x≤3),其图象上任意一点P(x0,y0)处切线的斜率k≤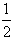 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;(3)当a=0,b=-1,方程2mf(x)=x2有唯一实数解,求正数m的值。
解:(1)依题意,知f(x)的定义域为(0,+∞),
当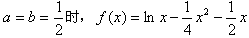 ,
,
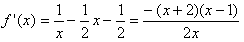 ,
,
令f′(x)=0, 解得x=1,(∵x>0),
因为g(x)=0有唯一解,所以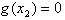 ,
,
当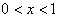 时,
时,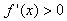 ,此时f(x)单调递增;
,此时f(x)单调递增;
当x>1时,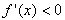 ,此时f(x)单调递减,
,此时f(x)单调递减,
所以f(x)的极大值为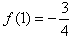 ,此即为最大值。
,此即为最大值。
(2)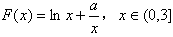 ,
,
则有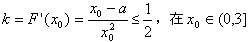 上恒成立,
上恒成立,
所以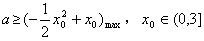 ,
,
当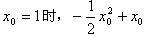 取得最大值
取得最大值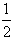 ,
,
所以a≥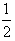 ;
;
(3)因为方程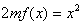 有唯一实数解,
有唯一实数解,
所以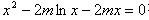 有唯一实数解,
有唯一实数解,
设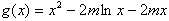 ,
,
则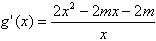 ,
,
令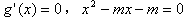 ,
,
因为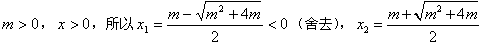 ,
,
当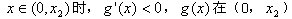 上单调递减;
上单调递减;
当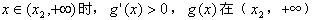 上单调递增;
上单调递增;
当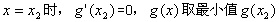 ,
,
则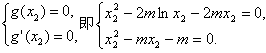 ,
,
所以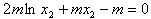 ,
,
因为m>0,
所以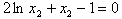 ,(*)
,(*)
设函数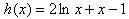 ,
,
因为当x>0时,h(x)是增函数,
所以h(x)=0至多有一解,
因为h(1)=0,
所以方程(*)的解为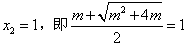 ,
,
解得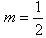 。
。
当
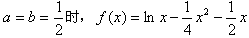 ,
,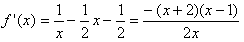 ,
,令f′(x)=0, 解得x=1,(∵x>0),
因为g(x)=0有唯一解,所以
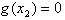 ,
,当
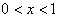 时,
时,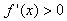 ,此时f(x)单调递增;
,此时f(x)单调递增;当x>1时,
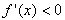 ,此时f(x)单调递减,
,此时f(x)单调递减,所以f(x)的极大值为
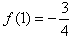 ,此即为最大值。
,此即为最大值。(2)
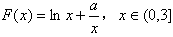 ,
,则有
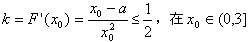 上恒成立,
上恒成立,所以
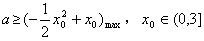 ,
,当
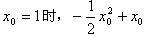 取得最大值
取得最大值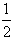 ,
,所以a≥
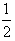 ;
;(3)因为方程
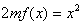 有唯一实数解,
有唯一实数解,所以
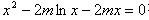 有唯一实数解,
有唯一实数解,设
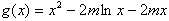 ,
,则
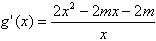 ,
,令
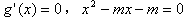 ,
,因为
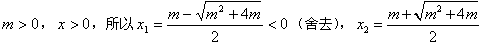 ,
,当
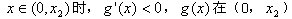 上单调递减;
上单调递减;当
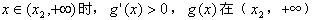 上单调递增;
上单调递增;当
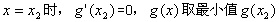 ,
,则
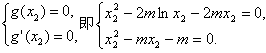 ,
,所以
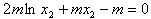 ,
,因为m>0,
所以
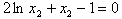 ,(*)
,(*)设函数
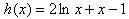 ,
,因为当x>0时,h(x)是增函数,
所以h(x)=0至多有一解,
因为h(1)=0,
所以方程(*)的解为
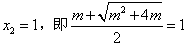 ,
,解得
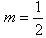 。
。
练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目