Question

（12分）在平面直角坐标系xOy中，已知圆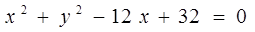的圆心为Q,过点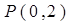且斜率为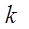的直线与圆Q相交于不同的两点A、B.

（1）求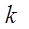的取值范围；

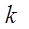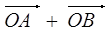（2）是否存在常数，使得向量与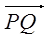共线？如果存在，求出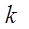的值；如果不存在，请说明理由。

 

Answer 1

【答案】

（1）k的取值范围为：

(2) ，,故没有符合题意的常数k.

【解析】解：（1）化为圆的标准方程为：，所以圆心为。

过点且斜率为k的直线方程为：，代入圆方程得：，整理得：----①

因为直线与圆有两个不同交点A,B，所以

解得，k的取值范围为：

（1）   设两交点的坐标分别为，

则由方程①可知，，---②

，---③

而，，所以。

若向量与，则必有

将②③式代入上式，解得。

由（1）可知，,故没有符合题意的常数k.