Question

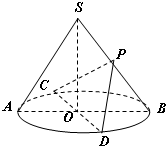如图，圆锥SO中，AB、CD为底面圆的两条直径，AB∩CD=O，且AB⊥CD，SO=OB=2，P为SB的中点．
（1）求证：SA∥平面PCD；
（2）求圆锥SO的表面积；
（3）求异面直线SA与PD所成的角正切值．

Answer 1

分析：（1）连接PO，利用三角形中位线性质，可得线线平行，从而可得线面平行；
（2）分别计算圆锥底面、侧面面积，即可求得圆锥SO的表面积；
（3）确定∠DPO为异面直线SA与PD所成的角，即可求得结论．

解答：（1）证明：连接PO，
∵P、O分别为SB、AB的中点，∴PO∥SA，
∵PO?平面PCD，SA?平面PCD
∴SA∥平面PCD；
（2）解：∵圆锥的底面半径r=2，母线长l=SB=2

2

，
S_底面=πr²=4π，S_侧面=πlr=4

2

π
S_圆锥表面=S_底面+S_侧面=4（

2

+1）π
（3）解：∵PO∥SA，∴∠DPO为异面直线SA与PD所成的角，
∵AB⊥CD，SO⊥CD，AB∩SO=O
∴CD⊥平面SOB．
∵PO?平面SOB，∴OD⊥PO，
在Rt△DOP中，OD=2，OP=

1

2

SA=

1

2

SB=

2

，
∴tan∠DPO=

OD

OP

=

2

∴异面直线SA与PD所成角的正切值为

2

．

点评：本题考查线面平行，考查表面积的计算，考查线线角，考查学生的计算能力，属于中档题．