题目内容
((本题满分14分)已知二次函数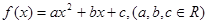 满足:对任意实数x,都有
满足:对任意实数x,都有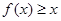 ,且当
,且当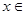 (1,3)时,有
(1,3)时,有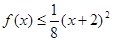 成立。
成立。
(1)证明: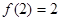 ;
;
(2)若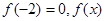 的表达式;
的表达式;
(3)在(2)的条件下,设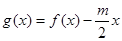 ,
,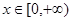 ,若
,若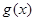 图上的点都位于直线
图上的点都位于直线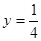 的上方,求实数m的取值范围。
的上方,求实数m的取值范围。
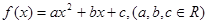 满足:对任意实数x,都有
满足:对任意实数x,都有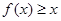 ,且当
,且当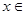 (1,3)时,有
(1,3)时,有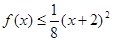 成立。
成立。(1)证明:
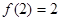 ;
;(2)若
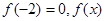 的表达式;
的表达式;(3)在(2)的条件下,设
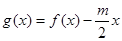 ,
,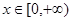 ,若
,若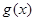 图上的点都位于直线
图上的点都位于直线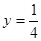 的上方,求实数m的取值范围。
的上方,求实数m的取值范围。解:(1)由条件知 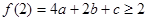 成立
成立
又∵取x=2时,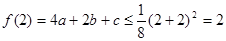 成立,
成立,
∴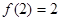 .
.
(2)∵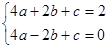 ∴
∴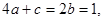 ∴
∴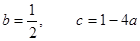 .
.
又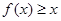 恒成立,即
恒成立,即 恒成立.
恒成立.
∴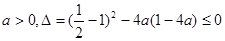 ,即
,即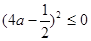
解出: ,
,
∴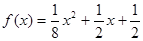 .
.
(3)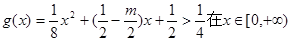 必须恒成立,
必须恒成立,
即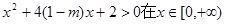 恒成立.
恒成立.
法一:①△<0,即 [4(1-m)]2-8<0,解得: ;
;
② 解出:
解出: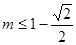 .
.
所以,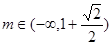 .
.
法二:当x=0时,2>0恒成立;
当 时要使
时要使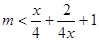 恒成立则
恒成立则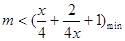
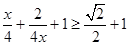 当且仅当
当且仅当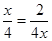 即
即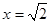 时取等号
时取等号
∴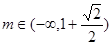
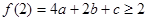 成立
成立又∵取x=2时,
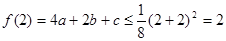 成立,
成立,∴
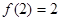 .
.(2)∵
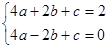 ∴
∴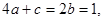 ∴
∴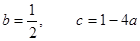 .
. 又
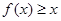 恒成立,即
恒成立,即 恒成立.
恒成立.∴
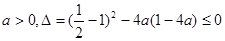 ,即
,即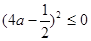
解出:
 ,
,∴
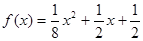 .
.(3)
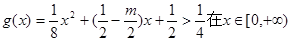 必须恒成立,
必须恒成立,即
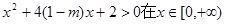 恒成立.
恒成立.法一:①△<0,即 [4(1-m)]2-8<0,解得:
 ;
;②
 解出:
解出: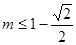 .
. 所以,
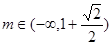 .
.法二:当x=0时,2>0恒成立;
当
 时要使
时要使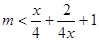 恒成立则
恒成立则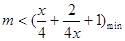
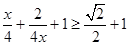 当且仅当
当且仅当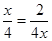 即
即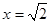 时取等号
时取等号∴
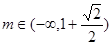
略

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
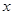 、
、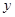 满足约束条件
满足约束条件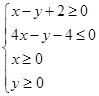 ,若目标函数
,若目标函数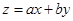
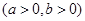 的最大值为6,则
的最大值为6,则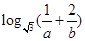 的最小值为
的最小值为
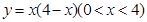 的最大值,并求
的最大值,并求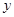 取最大值时相应的
取最大值时相应的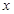 的值.
的值.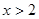 ,求
,求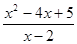 的最小值.
的最小值.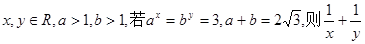 的最大值为( )
的最大值为( )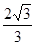
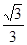
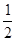
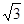
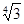
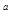 +3
+3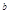 的最小值为( )
的最小值为( )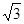
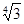
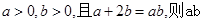 的最小值是( )
的最小值是( )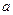 >0,
>0,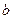 >0,且
>0,且 ,则
,则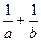 的最小值为
的最小值为