题目内容
等轴双曲线过点(1,2),则它的焦点坐标为
- A.(0,±6)
- B.(±6,0)
- C.(0,
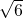 )
) - D.(
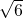 ,0)
,0)
C
分析:根据题中条件:“等轴双曲线过点(1,2)”先设出双曲线的标准方程 为x2-y 2=λ(λ≠0),根据双曲线过点A(1,2),代入方程确定a,,则双曲线方程可得.
解答:由题意知
可设双曲线的方程为 x2-y 2=λ(λ≠0),
又双曲线过A(1,2),
∴12-22=λ(λ≠0),
∴λ=-3
得双曲线方程:
则它的焦点坐标为(0,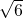 )
)
故选C.
点评:本题主要考查了双曲线的标准方程和双曲线的简单性质.属基础题.关键是需要利用双曲线的性质及题设条件找到a,b和c的关系,进而求得a和b.
分析:根据题中条件:“等轴双曲线过点(1,2)”先设出双曲线的标准方程 为x2-y 2=λ(λ≠0),根据双曲线过点A(1,2),代入方程确定a,,则双曲线方程可得.
解答:由题意知
可设双曲线的方程为 x2-y 2=λ(λ≠0),
又双曲线过A(1,2),
∴12-22=λ(λ≠0),
∴λ=-3
得双曲线方程:

则它的焦点坐标为(0,
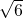 )
)故选C.
点评:本题主要考查了双曲线的标准方程和双曲线的简单性质.属基础题.关键是需要利用双曲线的性质及题设条件找到a,b和c的关系,进而求得a和b.

练习册系列答案
相关题目
等轴双曲线过点(1,2),则它的焦点坐标为( )
| A、(0,±6) | ||
| B、(±6,0) | ||
C、(0,±
| ||
D、(±
|
 )
) ,0)
,0)