题目内容
设f(x)是定义在R上的周期为2的偶函数,当x∈[0,1]时,f(x)=x-2x2,则f(x)在区间[0,2013]内零点的个数为( )A.2013
B.2014
C.3020
D.3024
【答案】分析:由题意可求得函数是一个周期函数,且周期为2,故可以研究出一个周期上的函数图象,再研究所给的区间包含了几个周期即可知道在这个区间中的零点的个数
解答:解:f(x)是定义在R上的周期为2的偶函数,又x∈[0,1]时,f(x)=x-2x2,要研究函数y=f(x)在区间[0,2013]零点个数,可将问题转化为y=f(x)与x轴在区间[0,2013]有几个交点,如图
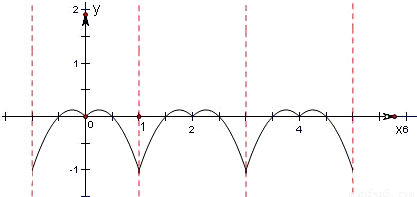
由图知,f(x)在区间[0,2013]内零点分别是: ,
, ,
, ,…,
,…,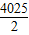 .共有2013个零点.
.共有2013个零点.
故选A.
点评:本题考查函数的零点,求解本题,关键是研究出函数f(x)性质,作出其图象,将函数y=f(x)在区间[0,2013]的零点个数的问题转化为交点个数问题是本题中的一个亮点,此一转化使得本题的求解变得较容易.
解答:解:f(x)是定义在R上的周期为2的偶函数,又x∈[0,1]时,f(x)=x-2x2,要研究函数y=f(x)在区间[0,2013]零点个数,可将问题转化为y=f(x)与x轴在区间[0,2013]有几个交点,如图

由图知,f(x)在区间[0,2013]内零点分别是:
 ,
, ,
, ,…,
,…,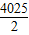 .共有2013个零点.
.共有2013个零点.故选A.
点评:本题考查函数的零点,求解本题,关键是研究出函数f(x)性质,作出其图象,将函数y=f(x)在区间[0,2013]的零点个数的问题转化为交点个数问题是本题中的一个亮点,此一转化使得本题的求解变得较容易.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |