题目内容
如图,P是双曲线 上的动点,F1、F2是双曲线的左右焦点,M是∠F1P
上的动点,F1、F2是双曲线的左右焦点,M是∠F1P
F2的平分线上一点,且F2M⊥MP。某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|= |NF1|,…,|OM|=a。类似地:P是椭圆
|NF1|,…,|OM|=a。类似地:P是椭圆 上的动点,F1、F2是椭圆的左右焦点, M是∠F1PF2的平分线上一点,且F2M⊥MP,则|OM|的取值范围是( )。
上的动点,F1、F2是椭圆的左右焦点, M是∠F1PF2的平分线上一点,且F2M⊥MP,则|OM|的取值范围是( )。
 上的动点,F1、F2是双曲线的左右焦点,M是∠F1P
上的动点,F1、F2是双曲线的左右焦点,M是∠F1PF2的平分线上一点,且F2M⊥MP。某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=
 |NF1|,…,|OM|=a。类似地:P是椭圆
|NF1|,…,|OM|=a。类似地:P是椭圆 上的动点,F1、F2是椭圆的左右焦点, M是∠F1PF2的平分线上一点,且F2M⊥MP,则|OM|的取值范围是( )。
上的动点,F1、F2是椭圆的左右焦点, M是∠F1PF2的平分线上一点,且F2M⊥MP,则|OM|的取值范围是( )。
练习册系列答案
相关题目
.如图,P是双曲线 上的动点,F1、
上的动点,F1、
F2是双曲线的焦点,M是 的平分线上一点,且
的平分线上一点,且
某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知 为
为
等腰三角形,且M为F2M的中点,得
|
 上的动点,F1、F2是椭圆的焦点,M是
上的动点,F1、F2是椭圆的焦点,M是 的平分线上一点,且
的平分线上一点,且 .则|OM|的取值范围是
.则|OM|的取值范围是
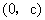


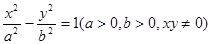 上的动点,
上的动点, 、
、 是双曲线的左右焦点,
是双曲线的左右焦点, 是
是 的平分线上一点,且
的平分线上一点,且 某同学用以下方法研究
某同学用以下方法研究 :延长
:延长 交
交 于点
于点 ,可知
,可知 为等腰三角形,且M为
为等腰三角形,且M为 的中点,得
的中点,得 类似地:P是椭圆
类似地:P是椭圆 上的动点,
上的动点, ,则
,则
 上的动点,F1、F2是双曲线的焦点,M是
上的动点,F1、F2是双曲线的焦点,M是 的平分线上一点,且
的平分线上一点,且 某同学用以下方法研究|OM|:延长
某同学用以下方法研究|OM|:延长 交
交 于点N,可知
于点N,可知 为等腰三角形,且M为
为等腰三角形,且M为 的中点,得
的中点,得 类似地:P是椭圆
类似地:P是椭圆 上的动点,F1、F2是椭圆的焦点,M是
上的动点,F1、F2是椭圆的焦点,M是 ,则|OM|的取值范围是
.
,则|OM|的取值范围是
.
 上的动点,F1、F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且
上的动点,F1、F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且 .某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2M的中点,得
.某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2M的中点,得 .类似地:P是椭圆
.类似地:P是椭圆 上的动点,F1、F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且
上的动点,F1、F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且 .则|OM|的取值范围是 .
.则|OM|的取值范围是 .
 上的动点,F1、F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且
上的动点,F1、F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且 .某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2M的中点,得
.某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2M的中点,得 .类似地:P是椭圆
.类似地:P是椭圆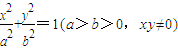 上的动点,F1、F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且
上的动点,F1、F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且 .则|OM|的取值范围是 .
.则|OM|的取值范围是 .