题目内容
（2013•宿迁一模）已知点P在圆x2+y2=1上运动，则P到直线3x+4y+15=0的距离的最小值为
2
2
．分析：先判断直线与圆的位置 关系，进而可知圆上的点到直线的最小距离为圆心到直线的距离减去圆的半径．
解答：解：∵x2+y2=1的圆心（0，0），半径为1
圆心到直线的距离为：d=
=3＞1
∴直线3x+4y+15=0与圆相离
∴圆上的点到直线的最小距离为：3-1=2
故答案为：2
圆心到直线的距离为：d=
| 15 |
| 5 |
∴直线3x+4y+15=0与圆相离
∴圆上的点到直线的最小距离为：3-1=2
故答案为：2
点评：本题主要考查了直线与圆的位置关系．考查了学生数形结合的思想，转化和化归的思想．
练习册系列答案
名校课堂系列答案
相关题目
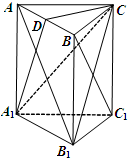（2013•宿迁一模）如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，BC=BB1，D为AB的中点．