题目内容
在△ABC中,∠BAC=120°,| |=2,|
|=2,| |=1,点P满足
|=1,点P满足 =λ
=λ (0≤λ≤1),则
(0≤λ≤1),则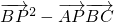 的取值范围是
的取值范围是
- A.[
 ,3]
,3] - B.[
 ,5]
,5] - C.[-2,
 ]
] - D.[
 ,5]
,5]
D
分析:由余弦定理得,BC2=AB2+AC2-2AB•ACcos∠BAC可求BC,然后由正弦定理得,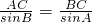 可求sinB,然后可求cosB,而
可求sinB,然后可求cosB,而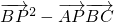 利用向量的数量积可转化为关于λ的二次函数,结合二次函数在闭区间上的最值即可求解
利用向量的数量积可转化为关于λ的二次函数,结合二次函数在闭区间上的最值即可求解
解答:在△ABC中,∠BAC=120°中,
根据余弦定理得,BC2=AB2+AC2-2AB•ACcos∠BAC
=
=
根据正弦定理得,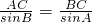
∴
∴sinB=
∴cosB=
从而有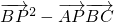 =
=
=
=
又0≤λ≤1,所以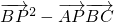 的取值范围是
的取值范围是
故选D
点评:本题主要考查了正弦定理、余弦定理在求解三角形中的应用,向量的数量积的应用及二次函数的性质的灵活应用是求解的关键
分析:由余弦定理得,BC2=AB2+AC2-2AB•ACcos∠BAC可求BC,然后由正弦定理得,
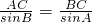 可求sinB,然后可求cosB,而
可求sinB,然后可求cosB,而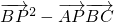 利用向量的数量积可转化为关于λ的二次函数,结合二次函数在闭区间上的最值即可求解
利用向量的数量积可转化为关于λ的二次函数,结合二次函数在闭区间上的最值即可求解解答:在△ABC中,∠BAC=120°中,
根据余弦定理得,BC2=AB2+AC2-2AB•ACcos∠BAC
=

=

根据正弦定理得,
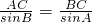
∴

∴sinB=

∴cosB=

从而有
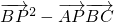 =
=
=

=

又0≤λ≤1,所以
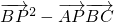 的取值范围是
的取值范围是
故选D
点评:本题主要考查了正弦定理、余弦定理在求解三角形中的应用,向量的数量积的应用及二次函数的性质的灵活应用是求解的关键

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
在△ABC中
等于( )
| a+b |
| a-b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,在△ABC中,
如图,在△ABC中,