题目内容
已知函数 的图象与
的图象与 的图象关于y轴对称.
的图象关于y轴对称.
(Ⅰ)求m的值;
(Ⅱ)若 (a∈R),试讨论函数g(x)的单调性.
(a∈R),试讨论函数g(x)的单调性.
解:(I)函数 的图象关于y轴对称的图象对应的解析式为:
的图象关于y轴对称的图象对应的解析式为:
 =
=
故m=1
(II)由(I)中f(x)=
故 =
=
 =
= +
+
∴g′(x)= -
- =
=
当a+1≤0,即a≤-1时,g′(x)≥0恒成立
此时g(x)在定义域(-∞,0)∪(0,+∞)上为增函数;
当a+1>0,即a>-1时,
若x∈(-∞,- )∪(
)∪( ,+∞)时,g′(x)>0;
,+∞)时,g′(x)>0;
若x∈(- ,
, )时,g′(x)<0;
)时,g′(x)<0;
此时g(x)在区间(-∞,- )和(
)和( ,+∞)上为增函数;
,+∞)上为增函数;
在区间(- ,
, )上为减函数;
)上为减函数;
分析:(I)根据函数对称变换法则,求出函数 的图象关于y轴对称的图象对应的解析式,进而可得m的值;
的图象关于y轴对称的图象对应的解析式,进而可得m的值;
(II)根据(I)中函数的解析式可得函数 的解析式,求出其导函数,分类讨论可得函数的单调性.
的解析式,求出其导函数,分类讨论可得函数的单调性.
点评:本题考查的知识点是指数函数的图象变换及函数的单调性,熟练掌握导数法求函数单调性的方法和步骤是解答的关键.
 的图象关于y轴对称的图象对应的解析式为:
的图象关于y轴对称的图象对应的解析式为: =
=
故m=1
(II)由(I)中f(x)=

故
 =
=
 =
= +
+
∴g′(x)=
 -
- =
=
当a+1≤0,即a≤-1时,g′(x)≥0恒成立
此时g(x)在定义域(-∞,0)∪(0,+∞)上为增函数;
当a+1>0,即a>-1时,
若x∈(-∞,-
 )∪(
)∪( ,+∞)时,g′(x)>0;
,+∞)时,g′(x)>0;若x∈(-
 ,
, )时,g′(x)<0;
)时,g′(x)<0;此时g(x)在区间(-∞,-
 )和(
)和( ,+∞)上为增函数;
,+∞)上为增函数;在区间(-
 ,
, )上为减函数;
)上为减函数;分析:(I)根据函数对称变换法则,求出函数
 的图象关于y轴对称的图象对应的解析式,进而可得m的值;
的图象关于y轴对称的图象对应的解析式,进而可得m的值;(II)根据(I)中函数的解析式可得函数
 的解析式,求出其导函数,分类讨论可得函数的单调性.
的解析式,求出其导函数,分类讨论可得函数的单调性.点评:本题考查的知识点是指数函数的图象变换及函数的单调性,熟练掌握导数法求函数单调性的方法和步骤是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象与x轴相切于点S(s,0).
的图象与x轴相切于点S(s,0). .
.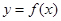 的图象与
的图象与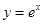 的图象关于直线
的图象关于直线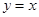 对称,则函数
对称,则函数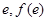 )处的切线方程为
.
)处的切线方程为
. 的图象与
的图象与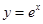 的图象关于直线
的图象关于直线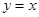 对称,则函数
对称,则函数 )处的切线方程为
.
)处的切线方程为
.