题目内容
已知数列{an}的前n项和为Sn,且点(n,Sn)在函数y=2x-1-2的图象上.
(I)求数列{an}的通项公式;
(II)设数列{bn}满足:b1=0,bn+1+bn=an,求数列{bn}的前n项和公式;
(III)在第(II)问的条件下,若对于任意的n∈N*不等式bn<λbn+1恒成立,求实数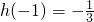 的取值范围.
的取值范围.
解:(I)由题意可知,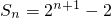 .
.
当n≥2时,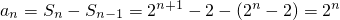 ,
,
当n=1时, 也满足上式,
也满足上式,
所以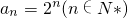 .…(3分)
.…(3分)
(II)由(I)可知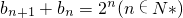 ,即
,即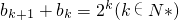 .
.
当k=1时,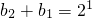 ,…①
,…①
当k=2时,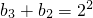 ,所以
,所以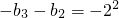 ,…②
,…②
当k=3时,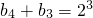 ,…③
,…③
当k=4时,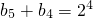 ,所以
,所以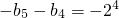 ,…④
,…④
…
…
当k=n-1时(n为偶数),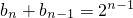 ,所以
,所以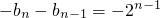 …n-1
…n-1
以上n-1个式子相加,得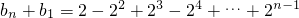
=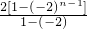 =
=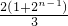 =
=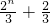 ,又b1=0,
,又b1=0,
所以,当n为偶数时,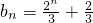 .
.
同理,当n为奇数时,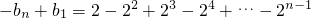
=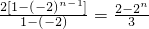 ,
,
所以,当n为奇数时,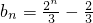 .…(6分)
.…(6分)
因此,当n为偶数时,数列{bn}的前n项和Tn=b1+b2+…+bn
=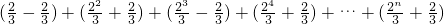
= =
=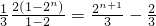 ;
;
当n为奇数时,数列{bn}的前n项和Tn=b1+b2+…+bn-1+bn
=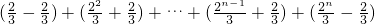
=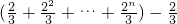 =
=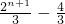 .
.
故数列{bn}的前n项和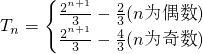 .…(8分)
.…(8分)
(III)由(II)可知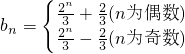 ,
,
①当n为偶数时,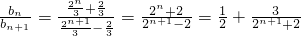 ,
,
所以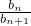 随n的增大而减小,
随n的增大而减小,
从而,当n为偶数时,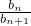 的最大值是
的最大值是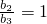 .
.
②当n为奇数时,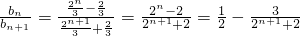 ,
,
所以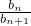 随n的增大而增大,且
随n的增大而增大,且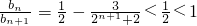 .
.
综上,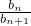 的最大值是1.
的最大值是1.
因此,若对于任意的n∈N*,不等式bn<λbn+1恒成立,只需λ>1,
故实数λ的取值范围是(1,+∞).…(13分)
分析:(I)由题意可知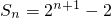 ,分当n=1,和n≥2两种情况,可得数列{an}的通项公式;
,分当n=1,和n≥2两种情况,可得数列{an}的通项公式;
(II)可得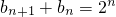 ,分n为奇数和n为偶数,由累加的方法,结合等比数列的求和公式可得答案;
,分n为奇数和n为偶数,由累加的方法,结合等比数列的求和公式可得答案;
(III)由(II)可知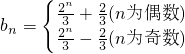 ,分当n为偶数和奇数时,考虑数列的单调性,可得
,分当n为偶数和奇数时,考虑数列的单调性,可得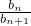 的最大值是1,进而可得结论.
的最大值是1,进而可得结论.
点评:本题考查数列的求和,涉及等差数列等比数列,以及分类讨论的思想,属中档题.
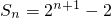 .
.当n≥2时,
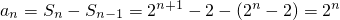 ,
,当n=1时,
 也满足上式,
也满足上式,所以
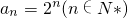 .…(3分)
.…(3分)(II)由(I)可知
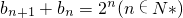 ,即
,即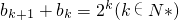 .
.当k=1时,
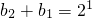 ,…①
,…①当k=2时,
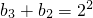 ,所以
,所以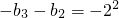 ,…②
,…②当k=3时,
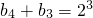 ,…③
,…③当k=4时,
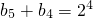 ,所以
,所以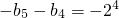 ,…④
,…④…
…
当k=n-1时(n为偶数),
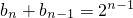 ,所以
,所以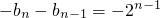 …n-1
…n-1以上n-1个式子相加,得
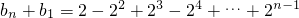
=
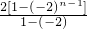 =
=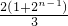 =
=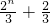 ,又b1=0,
,又b1=0,所以,当n为偶数时,
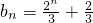 .
.同理,当n为奇数时,
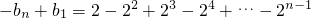
=
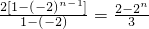 ,
,所以,当n为奇数时,
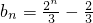 .…(6分)
.…(6分)因此,当n为偶数时,数列{bn}的前n项和Tn=b1+b2+…+bn
=
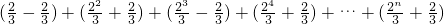
=
 =
=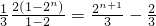 ;
;当n为奇数时,数列{bn}的前n项和Tn=b1+b2+…+bn-1+bn
=
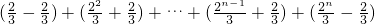
=
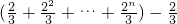 =
=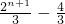 .
.故数列{bn}的前n项和
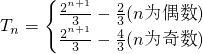 .…(8分)
.…(8分)(III)由(II)可知
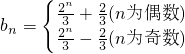 ,
,①当n为偶数时,
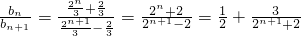 ,
,所以
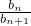 随n的增大而减小,
随n的增大而减小,从而,当n为偶数时,
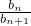 的最大值是
的最大值是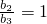 .
.②当n为奇数时,
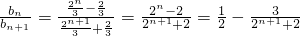 ,
,所以
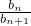 随n的增大而增大,且
随n的增大而增大,且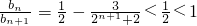 .
.综上,
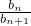 的最大值是1.
的最大值是1.因此,若对于任意的n∈N*,不等式bn<λbn+1恒成立,只需λ>1,
故实数λ的取值范围是(1,+∞).…(13分)
分析:(I)由题意可知
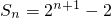 ,分当n=1,和n≥2两种情况,可得数列{an}的通项公式;
,分当n=1,和n≥2两种情况,可得数列{an}的通项公式;(II)可得
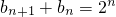 ,分n为奇数和n为偶数,由累加的方法,结合等比数列的求和公式可得答案;
,分n为奇数和n为偶数,由累加的方法,结合等比数列的求和公式可得答案;(III)由(II)可知
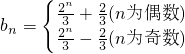 ,分当n为偶数和奇数时,考虑数列的单调性,可得
,分当n为偶数和奇数时,考虑数列的单调性,可得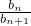 的最大值是1,进而可得结论.
的最大值是1,进而可得结论.点评:本题考查数列的求和,涉及等差数列等比数列,以及分类讨论的思想,属中档题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |