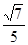题目内容
(本大题8分)定义运算 ,若函数
,若函数
 ,当
,当 时,
时, 的最大值与最小值的和为2.
的最大值与最小值的和为2.
(1).求 的值,并用五点法画出
的值,并用五点法画出 在长度为一个周期的区间内的简图。
在长度为一个周期的区间内的简图。
(2).求函数 的单调区间。
的单调区间。
 ,若函数
,若函数
 ,当
,当 时,
时, 的最大值与最小值的和为2.
的最大值与最小值的和为2.(1).求
 的值,并用五点法画出
的值,并用五点法画出 在长度为一个周期的区间内的简图。
在长度为一个周期的区间内的简图。(2).求函数
 的单调区间。
的单调区间。(1). 
 ;图略
;图略
(2) 单调递增区间为: ,单调递减区间为:
,单调递减区间为: ,其中
,其中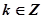

 ;图略
;图略 (2) 单调递增区间为:
 ,单调递减区间为:
,单调递减区间为: ,其中
,其中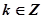
(1)先求出 ,然后根据最大值,最小值的和为2,求出a的值。再利用五点法作图即可。
,然后根据最大值,最小值的和为2,求出a的值。再利用五点法作图即可。
(2)利用正弦函数 的增区间
的增区间 和减区间
和减区间 求解即可。
求解即可。
解:(1). ……………………2分
……………………2分
 ;………………………………………………………2分
;………………………………………………………2分
图略 ………………………………………………………2分
(2) 单调递增区间为: ,单调递减区间为:
,单调递减区间为: ,其中
,其中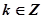 ………………………………………2分
………………………………………2分
 ,然后根据最大值,最小值的和为2,求出a的值。再利用五点法作图即可。
,然后根据最大值,最小值的和为2,求出a的值。再利用五点法作图即可。(2)利用正弦函数
 的增区间
的增区间 和减区间
和减区间 求解即可。
求解即可。解:(1).
 ……………………2分
……………………2分 ;………………………………………………………2分
;………………………………………………………2分图略 ………………………………………………………2分
(2) 单调递增区间为:
 ,单调递减区间为:
,单调递减区间为: ,其中
,其中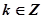 ………………………………………2分
………………………………………2分
练习册系列答案
相关题目
 的图像向右平移
的图像向右平移 个单位长度,所得图像经过点
个单位长度,所得图像经过点 则
则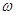 的最小值是( )
的最小值是( )

 ;
;
 ,
, 为偶函数时,求
为偶函数时,求 的值。
的值。 时,
时, 在
在 上是单调递增函数,求
上是单调递增函数,求 的取值范围。
的取值范围。 时,(其中
时,(其中 ,
, ),若
),若 ,且函数
,且函数 的图像关于点
的图像关于点 对称,在
对称,在 处取得最小值,试探讨
处取得最小值,试探讨 应该满足的条件。
应该满足的条件。 为锐角,且
为锐角,且 ,求
,求 的值;
的值; ,求
,求 的值.
的值.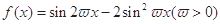
 的周期为
的周期为 ,求
,求 的值;
的值; 上为增函数,求满足条件的整数
上为增函数,求满足条件的整数
 ,sin(
,sin( )=-
)=- sin
sin 则cos
则cos =__________
=__________ ,那么tan x等于( )
,那么tan x等于( )



 的图象,这五个点可以分别是
的图象,这五个点可以分别是 ,
, ,
, , ,
, ,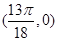 .
.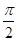 ),且sinα=
),且sinα=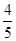 ,则cos2α等于( )
,则cos2α等于( )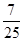 B—
B—