题目内容
已知l,m,n是三条不同的直线,α,β是不同的平面,则下列条件中能推出α⊥β的是( )
A.l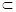 α,m α,m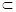 β,且l⊥m β,且l⊥m |
B.l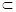 α,m α,m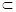 β,n β,n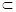 β,且l⊥m,l⊥n β,且l⊥m,l⊥n |
C.m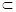 α,n α,n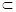 β,m//n,且l⊥m β,m//n,且l⊥m |
D.l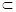 α,l//m,且m⊥β α,l//m,且m⊥β |
D
试题分析:对A.l
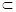 α,m
α,m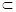 β,且l⊥m,如下图,α、β不垂直;对B.l
β,且l⊥m,如下图,α、β不垂直;对B.l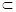 α,m
α,m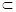 β,n
β,n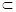 β,且l⊥m,
β,且l⊥m,l⊥n,如下图,α、β不垂直;
 ;
; ;
;对C.m
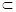 α,n
α,n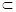 β,m//n,且l⊥m,直线l没有确定,则α、β的关系也不能确定;对D.l
β,m//n,且l⊥m,直线l没有确定,则α、β的关系也不能确定;对D.l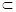 α,l//m,且m⊥β,则必有l⊥β,根据面面垂直的判定定理知,α⊥β.
α,l//m,且m⊥β,则必有l⊥β,根据面面垂直的判定定理知,α⊥β.
练习册系列答案
相关题目
 中,
中,
 ;
; 与直线BD所成的角
与直线BD所成的角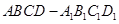 中,E为
中,E为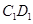 的中点.
的中点.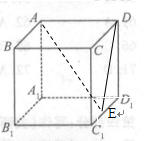
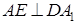 ;
;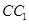 所成的角的正弦值.
所成的角的正弦值.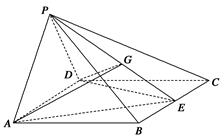
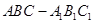 中,四边形
中,四边形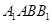 为菱形,
为菱形,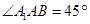 ,四边形
,四边形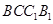 为矩形,若
为矩形,若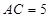 ,
,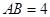 ,
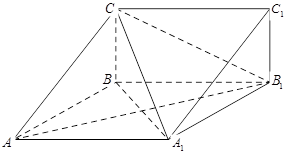
,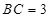 .
.
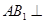 面
面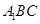 ;
;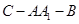 的余弦值;
的余弦值;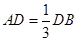 ,点C为圆O上一点,且
,点C为圆O上一点,且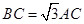 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.
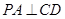 ;
;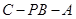 的余弦值.
的余弦值.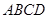 中,
中,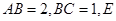 为
为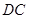 的中点,
的中点,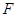 为线段
为线段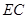 (端点除外)上一动点,现将
(端点除外)上一动点,现将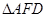 沿
沿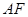 折起,使平面
折起,使平面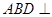 平面
平面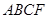 .在平面
.在平面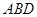 内过点
内过点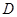 作
作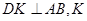 为垂足,设
为垂足,设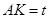 ,则
,则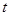 的取值范围是________
的取值范围是________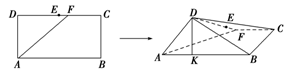
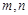 是两条不重合的直线,
是两条不重合的直线,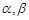 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: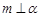 ,
,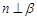 ,且
,且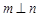 ,则
,则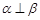 ;
;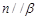 ,且
,且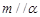 ,
,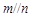 ,则
,则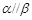 ;
;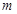 //直线
//直线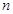 ,且
,且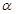 ,那么
,那么