题目内容
设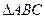 中的内角
中的内角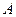 ,
,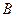 ,
,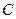 所对的边长分别为
所对的边长分别为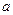 ,
,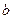 ,
,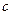 ,且
,且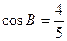 ,
,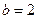 .
.
(1)当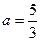 时,求角
时,求角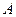 的度数;
的度数;
(2)求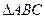 面积的最大值.
面积的最大值.
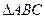 中的内角
中的内角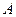 ,
,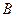 ,
,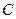 所对的边长分别为
所对的边长分别为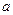 ,
,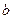 ,
,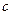 ,且
,且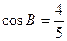 ,
,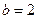 .
.(1)当
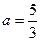 时,求角
时,求角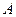 的度数;
的度数;(2)求
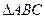 面积的最大值.
面积的最大值.(1)因为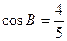 ,所以
,所以 . 因为
. 因为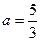 ,
,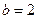 ,由正弦定理
,由正弦定理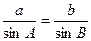 可得
可得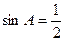 . 因为
. 因为 ,所以
,所以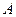 是锐角,所以
是锐角,所以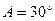 .
.
(2)因为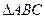 的面积
的面积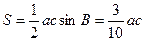 , 所以当
, 所以当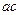 最大时,
最大时,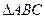 的面积最大.因为
的面积最大.因为 ,所以
,所以 .
.
因为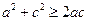 ,所以
,所以 ,所以
,所以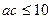 ,(当
,(当 时等号成立), 所以
时等号成立), 所以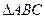 面积的最大值为
面积的最大值为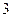 .
.
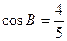 ,所以
,所以 . 因为
. 因为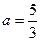 ,
,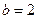 ,由正弦定理
,由正弦定理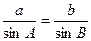 可得
可得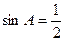 . 因为
. 因为 ,所以
,所以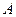 是锐角,所以
是锐角,所以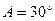 .
. (2)因为
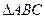 的面积
的面积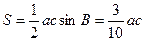 , 所以当
, 所以当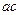 最大时,
最大时,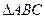 的面积最大.因为
的面积最大.因为 ,所以
,所以 .
. 因为
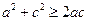 ,所以
,所以 ,所以
,所以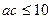 ,(当
,(当 时等号成立), 所以
时等号成立), 所以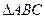 面积的最大值为
面积的最大值为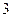 .
. 略

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
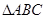 中,a=15,b=10,A=60°,则
中,a=15,b=10,A=60°,则 =
= 



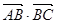 的值为( )
的值为( ) 中,
中, 分别为内角
分别为内角 的对边,且
的对边,且
 的大小;
的大小; 的最大值.
的最大值.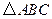 的周长为
的周长为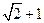 ,且
,且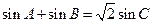 .
.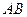 的长;
的长;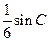 ,求角
,求角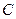 的度数.
的度数. 的边分别为a,b,c,且满足
的边分别为a,b,c,且满足
 ,则角A的大小为
,则角A的大小为  的面积是
的面积是 ,内角
,内角 所对边分别为
所对边分别为 ,
, .
. ,则
,则 的值是 ★ .
的值是 ★ . ,则
,则 ( )
( )