题目内容
已知角α的终边在第二象限，且与单位圆交于点
（1）求出a、sinα、cosα、tanα的值；
（2）求
的值．
解：（1）∵角α的终边在第二象限，且与单位圆交于点，故有a＜0，
=1．
解得 a=-
．
故 cosα=a=-，sinα=
，tanα=
=-
．
（2）=
=
tanα-1=-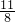
．
分析：（1）根据角α的终边在第二象限及单位圆的定义求得a的值，再根据任意角的三角函数的定义求得sinα、cosα、tanα的值
（2）利用诱导公式化、同角三角函数的基本关系，化简要求的式子为tanα-1，再把tanα的值代入求得结果．
点评：本题主要考查任意角的三角函数的定义，同角三角函数的基本关系、诱导公式的应用，属于基础题．
，故有a＜0，=1．解得 a=-
．故 cosα=a=-
，sinα=，tanα==-．（2）
==tanα-1=-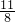．分析：（1）根据角α的终边在第二象限及单位圆的定义求得a的值，再根据任意角的三角函数的定义求得sinα、cosα、tanα的值
（2）利用诱导公式化、同角三角函数的基本关系，化简要求的式子为
tanα-1，再把tanα的值代入求得结果．点评：本题主要考查任意角的三角函数的定义，同角三角函数的基本关系、诱导公式的应用，属于基础题．
练习册系列答案
相关题目