题目内容
已知α、β为锐角, =(cosα,sinα),
=(cosα,sinα), =(cosβ,sinβ),
=(cosβ,sinβ), =(
=( ,-
,- ),
), =
= ,
, =
=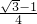 ,求角2β-α的值.
,求角2β-α的值.
解:∵ =(cosα,sinα)•(cosβ,sinβ)
=(cosα,sinα)•(cosβ,sinβ)
=cosαcosβ+sinαsinβ=cos(α-β)= ,①
,①
 =(cosα,sinα)•(
=(cosα,sinα)•( ,-
,- )
)
= cosα-
cosα- sinα=
sinα=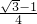 .②
.②
又∵0<α< ,0<β<
,0<β< ,∴-
,∴- <α-β<
<α-β< .
.
由①得α-β=± ,
,
由②得α= .由α、β为锐角,得β=
.由α、β为锐角,得β= .
.
③④
从而2β-α= π.
π.
分析:根据 和
和 的值,利用他们的坐标利用两角和公式分别求得cos(α-β)的值和sin(
的值,利用他们的坐标利用两角和公式分别求得cos(α-β)的值和sin( -α),进而联立求得α和β,则2β-α的值可得.
-α),进而联立求得α和β,则2β-α的值可得.
点评:本题主要考查了三角函数的恒等变换及化简求值,向量的基本运算.考查了考生综合运用所学知识的能力.
 =(cosα,sinα)•(cosβ,sinβ)
=(cosα,sinα)•(cosβ,sinβ)=cosαcosβ+sinαsinβ=cos(α-β)=
 ,①
,① =(cosα,sinα)•(
=(cosα,sinα)•( ,-
,- )
)=
 cosα-
cosα- sinα=
sinα=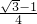 .②
.②又∵0<α<
 ,0<β<
,0<β< ,∴-
,∴- <α-β<
<α-β< .
.由①得α-β=±
 ,
,由②得α=
 .由α、β为锐角,得β=
.由α、β为锐角,得β= .
.③④
从而2β-α=
 π.
π.分析:根据
 和
和 的值,利用他们的坐标利用两角和公式分别求得cos(α-β)的值和sin(
的值,利用他们的坐标利用两角和公式分别求得cos(α-β)的值和sin( -α),进而联立求得α和β,则2β-α的值可得.
-α),进而联立求得α和β,则2β-α的值可得.点评:本题主要考查了三角函数的恒等变换及化简求值,向量的基本运算.考查了考生综合运用所学知识的能力.

练习册系列答案
相关题目
已知α,β,γ均为锐角,且tanα=
,tanβ=
,tanγ=
,则α,β,γ的和为( )
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知x,y为锐角,且满足cos x=
,cos(x+y)=
,则sin y的值是( )
| 4 |
| 5 |
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|