题目内容
已知a∈R,函数f(x)=x|x-a|.
(1)当a>2时,求函数y=f(x)在区间[1,2]上的最小值;
(2)若a=2时,方程f(x)=m有三个不同的实根,求m的取值范围.
解:(1)∵a>2,x∈[1,2],
∴f(x)=x(a-x)=-x2+ax=-(x- )2+
)2+ ,
,
当 ,即2<a≤3时,f(x)min=f(2)=2a-4,
,即2<a≤3时,f(x)min=f(2)=2a-4,
当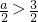 ,即a>3时,f(x)min=f(1)=a-1.
,即a>3时,f(x)min=f(1)=a-1.
∴f(x)= .
.
(2)当a=2时,f(x)= ,
,
如图为f(x)的图象,
∵方程f(x)=m有三个不同的实根,
∴m的取值范围是:0<m<1.
分析:(1)当a>2时,化简函数y=f(x)表达式,通过2<a≤3,a>3分别求出函数在区间[1,2]上的最小值即可;
(2)若a=2时,方程f(x)=m有三个不同的实根,画出函数的图象,即可求解m的取值范围.
点评:本题考查二次函数在闭区间上的最值,方程的根与函数的零点,考查数形结合,计算能力.

∴f(x)=x(a-x)=-x2+ax=-(x-
 )2+
)2+ ,
,当
 ,即2<a≤3时,f(x)min=f(2)=2a-4,
,即2<a≤3时,f(x)min=f(2)=2a-4,当
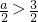 ,即a>3时,f(x)min=f(1)=a-1.
,即a>3时,f(x)min=f(1)=a-1.∴f(x)=
 .
.(2)当a=2时,f(x)=
 ,
,如图为f(x)的图象,
∵方程f(x)=m有三个不同的实根,
∴m的取值范围是:0<m<1.
分析:(1)当a>2时,化简函数y=f(x)表达式,通过2<a≤3,a>3分别求出函数在区间[1,2]上的最小值即可;
(2)若a=2时,方程f(x)=m有三个不同的实根,画出函数的图象,即可求解m的取值范围.
点评:本题考查二次函数在闭区间上的最值,方程的根与函数的零点,考查数形结合,计算能力.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目