题目内容
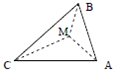 在△ABC中,∠C=90°,∠B=30°,AC=1,M为AB中点,将△ACM沿CM折起,使A、B间的距离为
在△ABC中,∠C=90°,∠B=30°,AC=1,M为AB中点,将△ACM沿CM折起,使A、B间的距离为 ,则点M到面ABC的距离为
,则点M到面ABC的距离为
- A.

- B.

- C.1
- D.

A
分析:由△AMC为等边三角形,取CM中点,则AD⊥CM,AD交BC于E,证明AE⊥平面BCM,利用等体积法,即可求得结论.
解答:由已知得AB=2,AM=MB=MC=1,BC= ,
,
由△AMC为等边三角形,取CM中点,则AD⊥CM,AD交BC于E,则AD= ,DE=
,DE= ,CE=
,CE= .
.
折起后,由BC2=AC2+AB2,知∠BAC=90°,
又cos∠ECA= ,∴AE2=CA2+CE2-2CA•CEcos∠ECA=
,∴AE2=CA2+CE2-2CA•CEcos∠ECA= ,于是AC2=AE2+CE2.
,于是AC2=AE2+CE2.
∴∠AEC=90°.
∵AD2=AE2+ED2,∴AE⊥平面BCM,即AE是三棱锥A-BCM的高,AE=
设点M到面ABC的距离为h,则
∵S△BCM=
∴由VA-BCM=VM-ABC,可得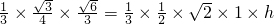 ,∴h=
,∴h=
故选A.
点评:本题考查由平面图形折成空间图形求其体积,考查点到平面距离的计算,求此三棱锥的高是解决问题的关键.
分析:由△AMC为等边三角形,取CM中点,则AD⊥CM,AD交BC于E,证明AE⊥平面BCM,利用等体积法,即可求得结论.
解答:由已知得AB=2,AM=MB=MC=1,BC=
 ,
,由△AMC为等边三角形,取CM中点,则AD⊥CM,AD交BC于E,则AD=
 ,DE=
,DE= ,CE=
,CE= .
.折起后,由BC2=AC2+AB2,知∠BAC=90°,
又cos∠ECA=
 ,∴AE2=CA2+CE2-2CA•CEcos∠ECA=
,∴AE2=CA2+CE2-2CA•CEcos∠ECA= ,于是AC2=AE2+CE2.
,于是AC2=AE2+CE2.∴∠AEC=90°.
∵AD2=AE2+ED2,∴AE⊥平面BCM,即AE是三棱锥A-BCM的高,AE=

设点M到面ABC的距离为h,则
∵S△BCM=

∴由VA-BCM=VM-ABC,可得
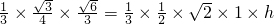 ,∴h=
,∴h=
故选A.
点评:本题考查由平面图形折成空间图形求其体积,考查点到平面距离的计算,求此三棱锥的高是解决问题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
