Question

已知空间四边形ABCD，P、Q分别是△ABC和△BCD的重心.求证：PQ∥平面ACD.

Answer 1

【探究】 欲证线面平行，须证线线平行，即要证明PQ与平面ACD中的某条直线平行，根据条件，此直线为AD，如图所示.

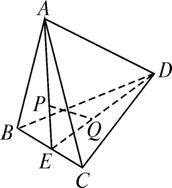
证明：取BC的中点E，∵P是△ABC的重心，连结AE，则AE：PE=3：1，连结DE，

∵Q为△BCD的重心，

∴DE：QE=3：1，

∴在△AED中，PQ∥AD.

又AD平面ACD，PQ平面ACD，

∴PQ∥平面ACD.

【规律总结】 (1)本例中构造直线AD与PQ平行，是充分借助于题目的条件：P、Q分别是△ABC和△BCD的重心，借助于比例的性质证明PQ∥AD，这种方法经常使用，注意把握.

(2)欲证线面平行，只须证线线平行，判定定理给我们提供了一种证明线面平行的方法，根据问题具体情况要熟练运用.