题目内容
下列四个命题中
①?x∈R,2x2-x+1>0;
②“x>1且y>2”是“x+y>3”的充要条件;
③函数y=
+
的最小值为2
其中假命题的为 ______(将你认为是假命题的序号都填上).
①?x∈R,2x2-x+1>0;
②“x>1且y>2”是“x+y>3”的充要条件;
③函数y=
| x2+2 |
| 1 | ||
|
其中假命题的为 ______(将你认为是假命题的序号都填上).
∵2x2-x+1=2(x-
)2+
>0恒成立
故①?x∈R,2x2-x+1>0为真命题;
若“x>1且y>2”成立,由不等式的性质,我们易得:“x+y>3”
但“x+y>3”时,“x>1且y>2”却不一定成立
故“x>1且y>2”是“x+y>3”的充分不必要条件,故②错误;
令t=
(t≥2)
则原函数可化为y=t+
(t≥2)
由函数y=t+
的单调性易知,[2,+∞)为函数的单调递增区间
故当t=2时,y有最小值
,故③错误.
故答案为:②③
| 1 |
| 4 |
| 7 |
| 8 |
故①?x∈R,2x2-x+1>0为真命题;
若“x>1且y>2”成立,由不等式的性质,我们易得:“x+y>3”
但“x+y>3”时,“x>1且y>2”却不一定成立
故“x>1且y>2”是“x+y>3”的充分不必要条件,故②错误;
令t=
| x2+2 |
则原函数可化为y=t+
| 1 |
| t |
由函数y=t+
| 1 |
| t |
故当t=2时,y有最小值
| 5 |
| 2 |
故答案为:②③

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
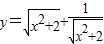 的最小值为2
的最小值为2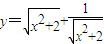 的最小值为2
的最小值为2