题目内容
判断并证明函数f(x)=
在(-∞,0)上的单调性.
| 1 | 1+x2 |
分析:利用定义判断函数的单调性,先设在所给区间上有任意两个自变量x1,x2,且x1<x2,再用作差法比较f(x1)与
f(x2)的大小,做差后,应把差的尽可能地分解为几个因式的乘积的形式,通过判断每一个因式的正负,来判断积的正负,最后得出结论.
f(x2)的大小,做差后,应把差的尽可能地分解为几个因式的乘积的形式,通过判断每一个因式的正负,来判断积的正负,最后得出结论.
解答:解:该函数在区间(-∞,0)上是增函数,
证明:设?x1,x2∈(-∞,0),且x1<x2,
因为f(x1)-f(x2)=
-
=
=
当x1<x2<0时,x2-x1>0,x1+x2<0,1+
>0,1+
>0;
所以f(x1)-f(x2)<0,即f(x1)<f(x2),
故该函数在区间(-∞,0)上是增函数.
证明:设?x1,x2∈(-∞,0),且x1<x2,
因为f(x1)-f(x2)=
| 1 | ||
1+
|
| 1 | ||
1+
|
| ||||
(1+
|
| (x1+x2)(x2-x1) | ||||
(1+
|
当x1<x2<0时,x2-x1>0,x1+x2<0,1+
| x | 2 1 |
| x | 2 2 |
所以f(x1)-f(x2)<0,即f(x1)<f(x2),
故该函数在区间(-∞,0)上是增函数.
点评:本题主要考查了定义法证明函数的单调性,做题时应该严格按照步骤去做.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
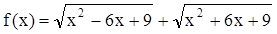
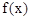 的单调区间.
的单调区间.