题目内容
已知函数F（x）=
，（x≠
），则F（
）+F（
）+…+F（
）=________．
3012
分析：观察已知函数可发现F（x）+F（1-x）=3，从而代入利用倒序相加可求
解答：因为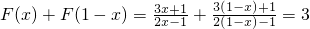
所以设S=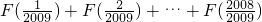
①
S=
②
①+②得：
=3×2008=6024，
所以S=3012．
故答案为：3012．
点评：本题主要考查了利用倒序求，这也是等差数列的求和公式的推导方法，其关键是F（x）+F（1-x）=3．
分析：观察已知函数可发现F（x）+F（1-x）=3，从而代入利用倒序相加可求
解答：因为
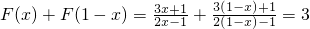
所以设S=
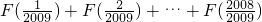①S=
②①+②得：
=3×2008=6024，所以S=3012．
故答案为：3012．
点评：本题主要考查了利用倒序求，这也是等差数列的求和公式的推导方法，其关键是F（x）+F（1-x）=3．
练习册系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|