Question

在平面直角坐标系内，将适合x＜y，|x|＜3，|y|＜3，且使关于t的方程(x3-y3)t4+(3x+y)t2+

1

x-y

=0没有实数根的点（x，y）所成的集合记为N，则由点集N所成区域的面积为．（　　）

• A．

  81

  4

• B．

  83

  4

• C．

  81

  5

• D．

  83

  5

Answer 1

分析：利用换元法，将方程转化为一元二次方程，利用转化后的方程无实根或有实根但均为负根，确定可行域，进而我们可以求出点集N所成区域的面积．

解答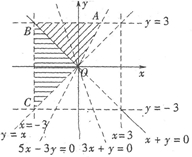：解：令u=t²，原方程化为(x3-y3)u2+(3x+y)u+

1

x-y

=0．①

△=(3x+y)2-4(x3-y3)• 1 x-y =5x2+2xy-3y2=(5x-3y)(x+y).

所给方程没有实根等价于方程①无实根或有实根但均为负根，
所以，

x＜y |x|＜3 |y|＜3 (5x-3y)(x+y)＜0

或

x＜y |x|＜3 |y|＜3 (5x-3y)(x+y)≥0 3x+y＜0.

点集N所成区域为图中阴影部分，
其面积为

S=S△ABO+S△BCO

= 1 2 × 24 5 ×3+ 1 2 ×6×3= 81 5 ．

故选C．

点评：这道题，难点在于所求区域的确定，关键在于利用换元法，将方程转化为一元二次方程，有技巧性．