题目内容
已知函数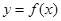 是定义在
是定义在 上的增函数,函数
上的增函数,函数 的图像关于点
的图像关于点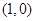 对称。若对任意的
对称。若对任意的 ,不等式
,不等式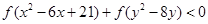 恒成立。则当
恒成立。则当 时,
时,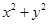 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
C
解析试题分析: 的图像关于点
的图像关于点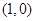 对称,所以
对称,所以 的图像关于点
的图像关于点 对称,
对称, 是奇函数
是奇函数 ,
,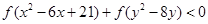 化为
化为 ,结合奇函数得
,结合奇函数得
 是定义在R上的增函数
是定义在R上的增函数
 ,点
,点 在圆
在圆 的内部,
的内部,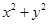 可看作
可看作 与
与 距离的平方,结合图像可知其最大值为49,最小值为13
距离的平方,结合图像可知其最大值为49,最小值为13
考点:函数单调性奇偶性等性质及数形结合法求两点间距离
点评:本题用到的函数性质是函数题目中最常用的性质,在解答过程中涉及到的知识点较多,要求学生对多版块的知识掌握都要熟练

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
设函数 与
与 的图象的交点为
的图象的交点为 ,则
,则 所在的区间是( )
所在的区间是( )
A. | B.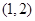 | C. | D. |
已知函数 是定义在实数集R上的不恒为零的偶函数,且对任意实数
是定义在实数集R上的不恒为零的偶函数,且对任意实数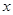 都有
都有 ,则
,则 的值是( )
的值是( )
A. | B. | C. | D. |
已知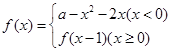 且函数
且函数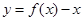 恰有3个不同的零点,则实数a的取值范围是( )
恰有3个不同的零点,则实数a的取值范围是( )
A.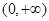 | B.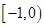 | C.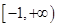 | D.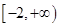 |
函数 ,
,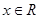
| A.是奇函数 | B.是偶函数 |
| C.既不是奇函数也不是偶函数 | D.既是奇函数也是偶函数 |
函数 的零点所在的区间为
的零点所在的区间为
A.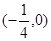 | B.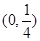 | C.(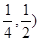 | D.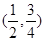 |
下列四组中 表示相等函数的是 ( )
表示相等函数的是 ( )
A. | B. |
C. | D. |
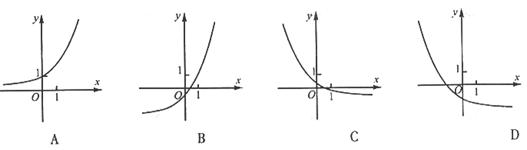
 1)的图象可能是
1)的图象可能是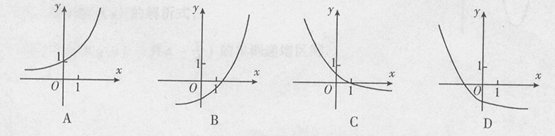
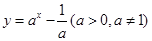 的图象可能是( )
的图象可能是( )