题目内容
设圆满足:①截y轴所得弦长为2;②被x轴分成的两段圆弧,其弧长之比为3∶1.在满足①②的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程.
解法一:设圆心P(a,b),若半径为r,则点P到x轴、y轴的距离分别为|b|、|a|.
又P截x轴所得劣弧对的圆心角为90°,知圆P截x轴所得弦长为
r,故r2=2b2.
又圆P截y轴所得弦长为2,
∴有r2=a2+1.∴2b2-a2=1.
又P到直线x-2y=0的距离为d=
,
∴5d2=|a-2b|2=a2+4b2-4ab≥a2+4b2-2(a2+b2)=2b2-a2=1.当且仅当a=b时等号成立,此时5d2=1,从而d取最小值.解得
r=
.∴方程为(x-1)2+(y-1)2=2或(x+1)2+
(y+1)2=2.
解法二:同解法一得d=
,
∴a-2b=±
d.
得a2=4b2±4
bd+5d2. ①
把a2=2b2-1代入①,整理得2b2±4
bd+5d2+1=0. ②
由Δ≥0,得d≥
.取等号时,b=±1.
再代入r2=2b2,得r2=2.
由r2=a2+1得a=±1.
又|a-2b|=1,
∴a、b同号.
∴方程为(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2.
练习册系列答案
相关题目
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分，请在答题纸指定区域内作答，解答应写出文字说明、证明过程或演算步骤．
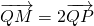的点M的轨迹为曲线C．
的点M的轨迹为曲线C．
的点M的轨迹为曲线C．