题目内容
下列函数中,在其定义域内既是增函数又是奇函数的是( )
分析:根据基本初等函数的单调性、奇偶性逐项判断即可.
解答:解:y=-
是奇函数,但在定义域(-∞,0)∪(0,+∞)内不单调,故排除A;
y=lnx递增,但定义域为(0,+∞),不关于原点对称,函数不具有奇偶性,故排除B;
y=ex递增,但不具有奇偶性,故排除C;
因为e-x递减,-e-x递增,又ex递增,x3递增,所以y=x3+ex-e-x递增,
令f(x)=x3+ex-e-x,则f(-x)=-x3-ex+e-x=-(x3+ex-e-x)=-f(x),
所以f(x)为奇函数,
故选D.
| 1 |
| x |
y=lnx递增,但定义域为(0,+∞),不关于原点对称,函数不具有奇偶性,故排除B;
y=ex递增,但不具有奇偶性,故排除C;
因为e-x递减,-e-x递增,又ex递增,x3递增,所以y=x3+ex-e-x递增,
令f(x)=x3+ex-e-x,则f(-x)=-x3-ex+e-x=-(x3+ex-e-x)=-f(x),
所以f(x)为奇函数,
故选D.
点评:本题考查函数奇偶性、单调性的判断,属基础题,定义是解决问题的基础,应熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
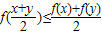 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数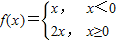
 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数