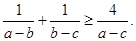题目内容
若关于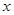 的方程
的方程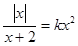 有四个不同的实数解,则实数
有四个不同的实数解,则实数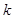 的取值范围为()
的取值范围为()
A. | B. | C.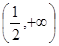 | D. |
解析试题分析:要求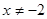 ,方程化为
,方程化为 ,
,
显然 满足上述方程,是方程的一个根
满足上述方程,是方程的一个根
若
则方程两边同除以 有
有
若 则方程变为
则方程变为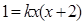 ,即
,即
若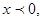 则方程变为
则方程变为 即
即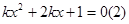
若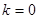 ,(1)(2)均无解。显然
,(1)(2)均无解。显然 不是(1)(2)的解
不是(1)(2)的解
若方程有四个不同的实数根,之前已得到 是原方程的根,则要求方程(1)(2)有3个根
是原方程的根,则要求方程(1)(2)有3个根
对(1)若判别式 ,则
,则 .
.
对(2)若判别式 ,解得
,解得 ,
,
前已分析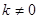
若 ,则(1)有两个不相等实根,两根之积为
,则(1)有两个不相等实根,两根之积为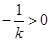 ,两根之和为
,两根之和为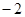 ,说明两根均为负值,但(1)方程前提条件是
,说明两根均为负值,但(1)方程前提条件是 ,因此
,因此 时方程(1)在
时方程(1)在 前提下无解,原方程不可能有4个不同的实数根。
前提下无解,原方程不可能有4个不同的实数根。
若 ,(1)方程无根,原方程不可能有4个不同的实数根。
,(1)方程无根,原方程不可能有4个不同的实数根。
若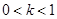 ,(2)方程无根,原方程不可能有4个不同的实数根。
,(2)方程无根,原方程不可能有4个不同的实数根。
若 ,方程(1)有两个不相等实根,两根之积为
,方程(1)有两个不相等实根,两根之积为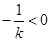 ,两根之和为
,两根之和为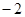 ,说明有一个正根一个负根,在
,说明有一个正根一个负根,在 前提下,只有一个正根,则要求(2)有两个不相等的负根。则
前提下,只有一个正根,则要求(2)有两个不相等的负根。则 .要求
.要求 .
.
对于(2)此时判别式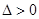 ,两根之和为
,两根之和为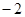 , 两根之积
, 两根之积 ,说明(2)有两个不相等的负根,之前要求
,说明(2)有两个不相等的负根,之前要求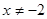 ,对(2),若
,对(2),若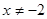 ,则
,则 ,显然
,显然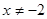 不是方程的根。
不是方程的根。
综上所述,要求 .
.
考点:含绝对值,未知字母方程的分类讨论.

练习册系列答案
相关题目
关于 的不等式
的不等式 (
( )的解集为
)的解集为 ,且
,且 ,则
,则 ( )
( )
A.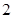 | B. | C.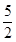 | D. |
(5分)(2011•广东)不等式2x2﹣x﹣1>0的解集是( )
A. | B.(1,+∞) | C.(﹣∞,1)∪(2,+∞) | D. ∪(1,+∞) ∪(1,+∞) |
不等式 的解集为( )
的解集为( )
A. | B. | C. | D. |
已知不等式 的解集为
的解集为 ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. |
C. | D. |
已知a∈[-1,1],不等式x2+(a-4)x+4-2a>0恒成立,则x的取值范围为( )
| A.(-∞,2)∪(3,+∞) | B.(-∞,1)∪(2,+∞) |
| C.(-∞,1)∪(3,+∞) | D.(1,3) |
[2014·皖南八校联考]不等式x2-2x+5≥a2-3a对任意实数x恒成立,则实数a的取值范围为( )
| A.[-1,4] |
| B.(-∞,-2]∪[5,+∞) |
| C.(-∞,-1]∪[4,+∞) |
| D.[-2,5] |
设A={x∈Z||x-2|≤5},则A中最小元素为( )
| A.2 |
| B.-3 |
| C.7 |
| D.0 |
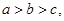 求证:
求证: