题目内容
已知数列{an}是等差数列,且满足:a1+a2+a3=6,a5=5;数列{bn}满足:bn-bn-1=an-1(n≥2,n∈N*),b1=1。
(1)求an和bn;
(2)记数列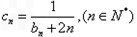 ,若{cn}的前n项和为Tn,求证
,若{cn}的前n项和为Tn,求证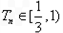 。
。
(1)求an和bn;
(2)记数列
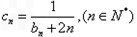 ,若{cn}的前n项和为Tn,求证
,若{cn}的前n项和为Tn,求证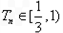 。
。解:(1)因为a1+a2+a3=6,a5=5,
所以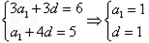
所以an=n;
又bn-bn-1=an-1=n-1,
(bn-bn-1)+(bn-1-bn-2)+(bn-2-bn-3)+…+(b3-b2)+(b2-b1)
=(n-1)+(n-2)+(n-3)+…+2+1得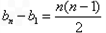
所以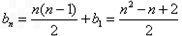
(2 )因为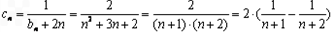
所以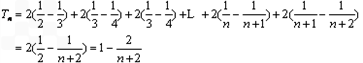
而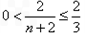 ,所以
,所以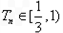
所以
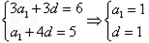
所以an=n;
又bn-bn-1=an-1=n-1,
(bn-bn-1)+(bn-1-bn-2)+(bn-2-bn-3)+…+(b3-b2)+(b2-b1)
=(n-1)+(n-2)+(n-3)+…+2+1得
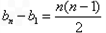
所以
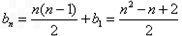
(2 )因为
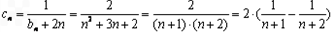
所以
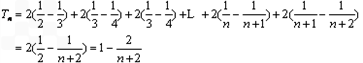
而
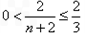 ,所以
,所以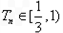

练习册系列答案
相关题目