题目内容
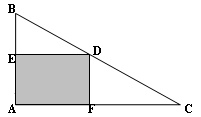
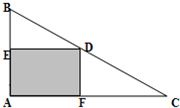Rt△ABC如图所示，直角边|AB|=3，|AC|=4．D点是斜边BC上的动点，DE⊥AB交于点E，DF⊥AC交于点F．设|AE|=x，四边形FDEA的面积为y，求y关于x的函数分析：由题意及图形，解决此问题的关键是求出AF的长度，由图形知，可求出CF，则AF可求，由此解题思路自明
解答：解：由图，tanC=
，D点是斜边BC上的动点，DE⊥AB交于点E，DF⊥AC交于点F．设|AE|=x，四边形FDEA是矩形，故DF=x，在直角三角形DFC中可得CF=
x，
由此得AF=4-CF=4-
x
故f（x）=AE×AF=x（4-
x）=-
x2+4x，x∈（0，3）
故答案为：f（x）=）=-
x2+4x，x∈（0，3）
| 3 |
| 4 |
| 4 |
| 3 |
由此得AF=4-CF=4-
| 4 |
| 3 |
故f（x）=AE×AF=x（4-
| 4 |
| 3 |
| 4 |
| 3 |
故答案为：f（x）=）=-
| 4 |
| 3 |
点评：本题考查根据实际问题选择函数类型，本题中求解函数解析式的关键是根据图形的几何特征求出AF的长度表达式，解题中注意抓住关键点．本题中的易错点是求完解析式后忘记写上定义域，做题时要切记．
练习册系列答案
相关题目
如图所示，Rt△A′B′C′为水平放置的△ABC的直观图，其中A′C′⊥B′C′，B′O′=O′C′=1，则△ABC的面积为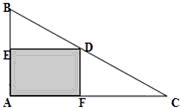
Rt△ABC如图所示，直角边|AB|=3，|AC|=4．D点是斜边BC上的动点，DE⊥AB交于点E，DF⊥AC交于点F．设|AE|=x，四边形FDEA的面积为y，求y关于x的函数
