Question

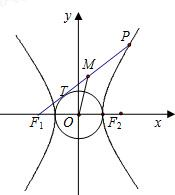如图，从双曲线

x2

9

-

y2

25

=1的左焦点F₁引圆x²+y²=9的切线，切点为T，延长F₁T交双曲线右支于P点．设M为线段F₁P的中点，O为坐标原点，则|F₁t|=

 

；|MO|-|MT|=

 

．

Answer 1

分析：先从双曲线

x2

9

-

y2

25

=1得：a=3，b=5．连OT，则OT⊥F₁T，在直角三角形OTF₁中，|F₁T|=b．连PF₂，M为线段F₁P的中点，O为坐标原点得出|MO|-|MT|=

1

2

|PF₂|-（

1

2

|PF₁|-|F₁T|），最后结合双曲线的定义即可得出答案．

解答：解：从双曲线

x2

9

-

y2

25

=1得：a=3，b=5．
连OT，则OT⊥F₁T，
在直角三角形OTF₁中，|F₁T|=

OF 1 2 -OT 2

=

c 2-a 2

=b=5．
连PF₂，M为线段F₁P的中点，O为坐标原点
∴OM=

1

2

PF₂，
∴|MO|-|MT|=

1

2

|PF₂|-（

1

2

|PF₁|-|F₁T|）=

1

2

（|PF₂|-|PF₁|）+5=5-a=2．
故答案为：5，2

点评：本题主要考查椭圆的定义及三角形中位线和直线与圆相切时应用勾股定理．解答的关键是熟悉双曲线的定义的应用，直线与圆的位置关系以及三角形中的有关结论．