题目内容

过抛物线x²=4y的焦点F作倾斜角为30°的直线，与抛物线分别交于A、B两点（A在y轴左侧），则 $数学公式$ =________．

$\text{[math]}$
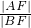分析：点斜式设出直线l的方程，代入抛物线方程，求出A，B两点的纵坐标，利用抛物线的定义 $\text{[math]}$ ，求出 $\text{[math]}$ 的值．
解答：设直线l的方程为：x= $\text{[math]}$ （y-1），再设A（x₁，y₁），B（x₂，y₂），
由 $\text{[math]}$ ∴ $\text{[math]}$ ，
从而， $\text{[math]}$ ．
故答案为 $\text{[math]}$ ．
点评：本题考查抛物线的定义、标准方程，以及简单性质的应用，利用抛物线的定义 $\text{[math]}$ ，是解题的关键．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

过抛物线x²=4y的焦点F作倾斜角为30°的直线，与抛物线分别交于A、B两点（A在y轴左侧），则

过抛物线x²=4y的焦点F作直线交抛物线于P₁（x₁、y₁），P₂（x₂、y₂）两点，若y₁+y₂=6，则|P₁P₂|的值为（　　）

过抛物线x²=4y的焦点F作直线交抛物线于P₁（x₁，y₁）P2（x₂，y₂）两点，若y₁+y₂=6，求|P₁P₂|的值．

如图，过抛物线x²=4y的对称轴上任一点P（0，m）（m＞0）作直线与抛物线交于A（x₁，y₁），B（x₂，y₂）两点．
（I）若

(λ∈R)，证明：λ=-

；
（II）在（I）条件下，若点Q是点P关于原点对称点，证明：

)；
（III）设直线AB的方程是x-2y+12=0，过A，B两点的圆C与抛物线在点A处有共同的切线，求圆C的方程．

已知过抛物线x²=4y的焦点，斜率为k（k＞0）的直线l交抛物线于A（x₁，y₂），B（x₂，y₂）（x₁＜x₂）两点，且|AB|=8．
（1）求直线l的方程；
（2）若点C（x₃，y₃）是抛物线弧AB上的一点，求△ABC面积的最大值，并求出点C的坐标．