题目内容
过x轴上一点P向圆C:x2+(y-2)2=1作切线,切点分别为A、B,则△PAB面积的最小值是________.

分析:由圆的方程为求得圆心C(0,2)、半径r为:1,设点P(a,0),利用两点间距离公式求得PC=
 ,利用勾股定理求得PA=PB=
,利用勾股定理求得PA=PB=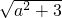 ,解直角三角形求得sin∠APB,利用面积公式求得△PAB面积,利用换元法以及函数的单调性求得△PAB面积的最小值.
,解直角三角形求得sin∠APB,利用面积公式求得△PAB面积,利用换元法以及函数的单调性求得△PAB面积的最小值.解答:∵圆的方程为::x2+(y-2)2=1
∴圆心C(0,2)、半径r为:1
设点P(a,0),则PC=
 ,PA=PB=
,PA=PB=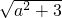 ,
,sin∠APB=2
 =
= ,
,∴
 sin∠APB=
sin∠APB= ,
,令
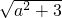 =t,t
=t,t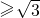 ,
,∴
 =
= 在(
在( ,+∞)上单调递增,
,+∞)上单调递增,∴当t=
 时,△PAB面积有最小值为
时,△PAB面积有最小值为 .
.故答案为:
 .
.点评:本题主要考查直线与圆的位置关系,以及解直角三角形和三角形的面积公式等基础知识,综合性强,要求学生对知识掌握到位,并且你灵活应用,求出三角形的面积后,又转化为函数求最小值问题,体现了转化的思想和函数的思想,也很好的考查了运算能力.此题属难题.

练习册系列答案
相关题目