题目内容
设F1、F2分别为椭圆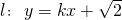 的左、右焦点,过F1的直线交椭圆于M、N两点,则△MNF2的周长为
的左、右焦点,过F1的直线交椭圆于M、N两点,则△MNF2的周长为
- A.
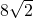
- B.

- C.8
- D.4
A
分析:根据△MNF2的周长为( MF1+MF2 )+(NF1+NF2)=2a+2a=4a,求得结果.
解答:△MNF2的周长为( MF1+MF2 )+(NF1+NF2)=2a+2a=4a=4×2 =8
=8 ,
,
故选 A.
点评:本题考查椭圆的定义、标准方程,得到△MNF2的周长为( MF1+MF2 )+(NF1+NF2)=2a+2a,是
解题的关键.
分析:根据△MNF2的周长为( MF1+MF2 )+(NF1+NF2)=2a+2a=4a,求得结果.
解答:△MNF2的周长为( MF1+MF2 )+(NF1+NF2)=2a+2a=4a=4×2
 =8
=8 ,
,故选 A.
点评:本题考查椭圆的定义、标准方程,得到△MNF2的周长为( MF1+MF2 )+(NF1+NF2)=2a+2a,是
解题的关键.

练习册系列答案
相关题目
 (a>b>0)的左、右两个焦点,椭圆C上的点
(a>b>0)的左、右两个焦点,椭圆C上的点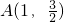 到两点的距离之和等于4.
到两点的距离之和等于4. 求|PQ|的最大值.
求|PQ|的最大值.