题目内容
【题目】对于数列![]() :
:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,若不改变
,若不改变![]() ,仅改变
,仅改变![]() 、
、![]() 、
、![]() 、
、![]() 中部分项的符号(可以都不改变),得到的新数列
中部分项的符号(可以都不改变),得到的新数列![]() 称为数列
称为数列![]() 的一个生成数列,如仅改变数列
的一个生成数列,如仅改变数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的第二、三项的符号,可以得到一个生成数列:
的第二、三项的符号,可以得到一个生成数列:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .已知数列
.已知数列![]() 为数列
为数列![]() 的生成数列,
的生成数列,![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)写出![]() 的所有可能的值;
的所有可能的值;
(2)若生成数列![]() 的通项公式为
的通项公式为 ,求
,求![]() ;
;
(3)用数学归纳法证明:对于给定的![]() ,
,![]() 的所有可能值组成的集合为
的所有可能值组成的集合为![]() .
.
【答案】(1)![]() 、
、![]() 、
、![]() 、
、![]() ;(2)
;(2)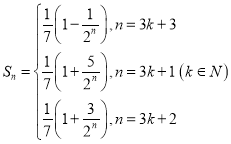 ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)根据生成数列定义,可知当![]() 时,
时,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中取值,由此给出
中取值,由此给出![]() 的所有可能的情况,即可计算出
的所有可能的情况,即可计算出![]() 的所有可能值;
的所有可能值;
(2)利用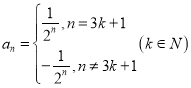 ,分
,分![]() 、
、![]() 、
、![]() 三种情况讨论,利用分组求和与等比数列的求和公式即可求得
三种情况讨论,利用分组求和与等比数列的求和公式即可求得![]() ;
;
(3)利用数学归纳法证明:①当![]() 时命题成立;②假设当
时命题成立;②假设当![]() 时,
时,![]() ,证明出
,证明出![]() ,结合归纳原理即可证明出结论成立.
,结合归纳原理即可证明出结论成立.
(1)由题意得![]() ,
,![]() ,
,
根据生成数列的定义,可得![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因此,![]() 所有可能的取值为
所有可能的取值为![]() 、
、![]() 、
、![]() 、
、![]() ;
;
(2)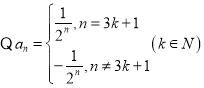 ,
,
当![]() 时,
时,![]()
![]()
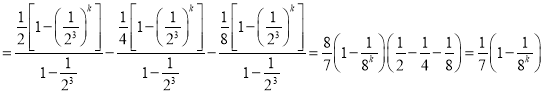
![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
综上所述: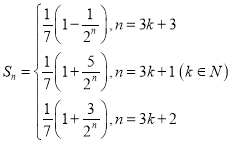 ;
;
(3)利用数学归纳法证明:
①当![]() 时,
时,![]() ,命题成立;
,命题成立;
②假设当![]() 时,命题成立,即
时,命题成立,即![]() 所有可能值的集合为
所有可能值的集合为![]() .
.
由假设得![]() .
.
则当![]() 时,
时,![]()
![]() .
.
即![]() 或
或![]() ,
,
即![]() ,
,
![]() 当
当![]() 时,命题成立.
时,命题成立.
由①②知,对于给定的![]() ,
,![]() 的所有可能值组成的集合为
的所有可能值组成的集合为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目